Amiga “packed” – 9: Il Blitter – Generazione maschere, costi, AGA

Introdotta la meravigliosa primitiva grafica chiamata cookie-cut in gergo amighista, passiamo ad analizzare l’algoritmo centrale dell’implementazione packed.

Il Blitter – inserimento di un oggetto grafico “mascherato” – Generazione delle maschere

L’esempio esposto nel precedente articolo dovrebbe aver contribuito a far chiarezza, fatta eccezione sull’elemento cardine del meccanismo spiegato: la generazione delle maschere. A parole sembra molto semplice, ma il diavolo si nasconde nei dettagli, come si suol dire. Infatti la parte più complicata del nuovo algoritmo risulta proprio nell’implementazione di questo meccanismo e non è affatto chiaro come si dovrebbe procedere concretamente, poiché c’è da tenere conto sia della specifica profondità di colore sia dal fatto che per essa è possibile generare maschere di lunghezza diversa (a seconda del numero di bit utilizzati).

L’idea che m’è venuta in mente è di utilizzare dei multiplexer (abbreviati come mux) in cascata, che attingano dai bit della sorgente A (da un minimo di due per grafica a 64 colori fino a un massimo di otto per 4 colori, come da prima tabella nel pezzo precedente), e dai quali vengano fuori i bit della maschera generata, utilizzando la profondità di colore per selezionare quali bit in ingresso debbano poi finire in uscita. Il che dice molto e nulla allo stesso tempo, in quanto rimane ancora oscuro come tutto ciò dovrebbe funzionare, alla fine.

Riporto, per comodità, dalla pagina di Wikipedia l’immagine di un mux 8-a-1 (otto ingressi e una sola uscita, che richiede tre linee addizionali per selezionare quale delle 8 linee in ingresso debba finire nell’unica uscita):

Nel nostro caso non serve un mux di questa complessità, perché le linee in ingresso sono soltanto 5 (dunque è possibile realizzare specificamente un mux a 5-a-1, eventualmente combinando un mux 4-a-1 e un altro 2-a-1), ma non avendo trovato immagini o esempi di questo tipo ho preferito utilizzare il classico mux 8-a-1.

Sempre dalla prima tabella del precedente articolo, sappiamo che possiamo generare maschere con massimo 20 bit (per la profondità di colore di 5 bit: le altre generano maschere con meno bit), per cui dovremo utilizzare 20 mux 5-a-1 per poter implementare questa parte del meccanismo.

Non avendo mai usato software di progettazione di circuiti mi limiterò a illustrare, al solito tramite una tabella, l’uscita prodotta da ogni mux (colonna Mux (bit)) in base alla profondità di colore selezionata (colonne Depth 2 .. Depth 6), in modo da far comprendere in che modo tutta questa parte del circuito vada implementata, partendo dal primo mux (#19: quello che produce il bit più significativo, ossia il ventesimo) e ricordando che i bit presenti nel buffer vadano presi partendo dal più significativo (#7):

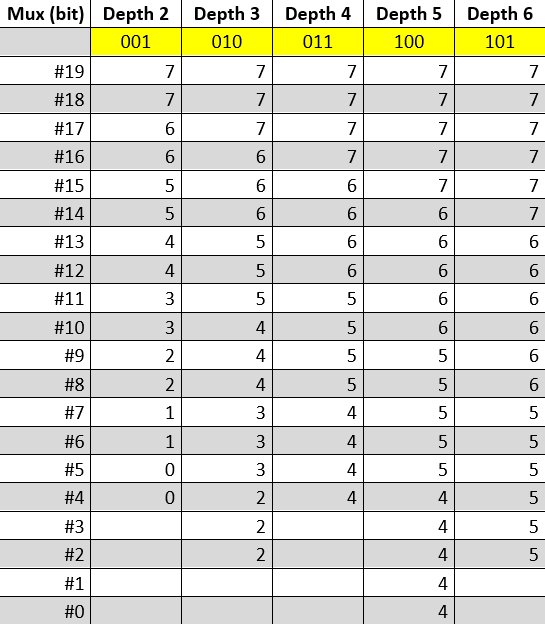
Le colonne Depth rappresentano quale bit del buffer debba essere utilizzato per la specifica linea di ingresso per quel determinato mux (riga). Le celle vuote indicano che l’uscita è forzata a zero, poiché nessun bit del buffer viene usato per quella specifica profondità di colore.

Per fare un esempio concreto, prendiamo l’undicesimo mux (#10) e vediamo che la sua prima linea d’ingresso debba essere collegata al bit #3 del buffer, mentre la seconda al bit #4, la terza al #5, e infine la quarta e la quinta entrambe al bit #6. A questo punto se il Blitter è impostato per una profondità di colore pari a 3 bit, il mux #10 riceverà il valore 010 nelle sue tre linee di selezione, che comporterà l’uscita del bit #4 del buffer.

Un’ultima precisazione è doverosa, in quanto risulta evidente che i casi relativi ai primi due mux (#19 e #18) siano banali, in quanto l’uscita è sempre determinata dal bit #7 del buffer. Quindi non serve un mux: è sufficiente collegare direttamente il bit #7 del buffer al bit #19 della maschera generata. Similmente, gli ultimi due casi (mux #1 e #0) sono abbastanza banali da non richiedere anche qui un mux: è sufficiente collegare il bit #4 del buffer a una porta and in cui l’altro ingresso è collegato a comparatore che dia come risultato 1 se la profondità di colore è stata impostata a 100 o 0 altrimenti.

Credo non sia necessario aggiungere altro, perché adesso dovrebbe essere ben chiaro in che modo vengono generate le varie maschere a seconda della profondità di colore selezionata (la colonna relativa alla profondità di colore determina quali ingressi saranno usati nei vari mux).

Il Blitter – inserimento di un oggetto grafico “mascherato” – Costi di implementazione

Conclusa la spiegazione del nuovo algoritmo utilizzato per “disegnare” i cosiddetti BOB (Blitter OBject. Gli “equivalenti” degli sprite, ma generati via software tramite il Blitter), rimane da fare i conti che, come prevedibile, non sono trascurabili (è tutta logica che si va ad aggiungere a quella che implementa già il Blitter) e riguardano i seguenti componenti necessari alla sua concreta implementazione.

• Servono 3 bit (3 celle SRAM) per indicare la profondità di colore utilizzata (meno uno: zero indicherà pixel di 1 bit = 2 colori, uno indicherà pixel di 2 bit = 4 colori, e così via. In questo modo il caso del singolo bitplane non subirà alcun cambiamento, in quanto il valore usato allo scopo è zero e verrà, quindi, utilizzata l’implementazione originale). Il registro BLTCON1 del Blitter ha alcuni bit liberi / riservati che possono essere usati allo scopo (sono sempre a zero), per cui non c’è alcun costo da sostenere (almeno qui, ma è niente rispetto a ciò serve per il resto).
• Per eseguire lo shift (a sinistra) dei bit del buffer serve un barrel shifter a 8 bit con spostamenti fino a 7 posizioni, e idem per la rotazione (a sinistra) del byte interno.
• Sempre per la gestione di questi due elementi abbiamo visto col controllore video che servono 4 sommatori/sottrattori a 4 bit (equivalenti a un totale di 4 x 6 = 24 celle SRAM). Il quinto sommatore per la coda FIFO non serve, perché in questo caso la sua implementazione risulta molto semplificata; servono, infatti, soltanto 2 bit (2 celle SRAM) che indicano quali dei due byte della coda contengono dati), ma in ogni caso sono necessari 2 x 8 = 16 bit per memorizzare i due byte della coda FIFO. Ovviamente servono anche 4 bit per memorizzare il numero di bit nel buffer e altrettanti per il numero di bit nel byte interno Quindi complessivamente sono necessarie un totale di 24 + 2 + 16 + 2 x 4 = 50 celle SRAM.
• Memorizzare il numero di bit che sono rimasti dalla precedente generazione della maschera richiede 3 bit (rimangono, al massimo, 5 bit per profondità di colore pari a 6 bit), pari a 3 celle SRAM.
• Per sapere se utilizzare 5 o 6 bit (sempre nel caso di 8 colori, ma è lo stesso per qualunque profondità di colore) dal buffer è necessario sommare il numero di bit generati nel caso di meno bit utilizzati (dunque 15 per grafica a 8 colori, ad esempio). In tal caso servirà un registro in cui memorizzare i 4 bit necessari (i valori vanno da 12 a 16, ma il caso 16 può essere trattato come zero e col quinto bit ricavato negando il quarto. Quindi i valori da 12 a 15 vengono memorizzati così come sono, mentre il 16 verrà memorizzato come zero). Un intero registro significa allocare 16 bit, pari a 16 celle SRAM. Similmente, serviranno 4 bit per memorizzare il numero di bit generati nel caso di più bit utilizzati; anche qui non serve memorizzare il quinto bit (perché i valori vanno da 16 a 20, in questo caso), perché è sempre a 1. Anche questi 4 bit vanno a finire nel nuovo registro a 16 bit.
• Serve un sommatore a 4 bit per sommare il numero di bit rimasti dalla precedente maschera col minimo numero di bit che si possono generare (come da punto precedente), equivalente a circa 6 celle SRAM. Da notare che il bit di riporto di questa somma va utilizzato per eseguire l’or con la negazione del 4° bit del minimo numero di bit generabili (vedere sempre sopra per la motivazione): se il risultato sarà 1, allora vuol dire che i bit totali (quelli rimasti dalla precedente maschera e il numero minimo di bit generabili) sono almeno 16.
• Quattro bit sono necessari per memorizzare il numero minimo di bit che si possono prelevare dalla sorgente A (buffer A) per generare la nuova maschera, e altrettanti bit sono necessari per il numero massimo di bit. In entrambi i casi non sono necessarie altre risorse, perché si possono utilizzare i bit liberi nel nuovo registro a 16 bit di cui ho parlato sopra. La scelta fra questi due valori avviene tramite il bit calcolato alla fine del punto precedente; ciò è importante perché bisogna poi sapere quanti bit bisogna eliminare dal buffer.
• Combinare i bit rimasti dalla precedente maschera (che possono essere al massimo 5, per grafica a 64 colori) con quelli della nuova maschera (che possono essere al massimo 20, per grafica a 32 colori) richiede l’uso di un barrel shifter da 24 bit (concatenando al massimo 5 bit da quelli rimasti con quelli nuovi generati) con spostamento a destra di al massimo 5 posizioni (sono sempre i bit rimasti a dominare). Servono anche i 24 bit necessari per conservare il contenuto dell’operazione, che richiedono, pertanto, 24 celle SRAM.
• Un sommatore a 3 bit è necessario per calcolare la somma del numero di bit rimasti col numero di bit generati. Si possono ignorare gli altri bit, perché verranno poi estratti ed eliminati i 16 bit che andranno combinati con gli altrettanti delle sorgenti B e C, per cui sarà necessario sottrarre 16 al risultato di questa somma. Un sommatore a 3 bit richiede tre full-adder; poiché un full-adder richiede 9 transistor, ne serviranno 3 x 9 = 27 in totale, pari a circa 5 celle SRAM.
• Infine serve implementare la logica di generazione delle maschere che, come visto prima, richiede l’uso di 16 mux da 5-a-1. In realtà e come visto dalla tabella qui sopra, sono i casi semplici da implementare, che non richiedono la complessità di un intero mux 5-a-1; a motivo di ciò ritengo sia ragionevole assumere che la logica ad hoc richiesta per implementare questi 16 mux possa avere un costo implementativo simile a quello di 16 mux 4-a-1. Rimane, in ogni caso, il problema di determinare quanti transistor saranno impiegati (e, quindi, quante celle SRAM, visto che ho preso queste come “unità di misura” del consumo di risorse), che non sembra di facile soluzione (almeno per me che non sono del campo). Infatti se per un mux 4-a-1 è facile trovare schemi di implementazione che usano porte logiche, le porte logiche a loro volta possono essere implementate in diversi modi e con un numero diverso di transistor, per cui il calcolo dei transistor utilizzati per un tale mux rimane in sospeso (ma riporto qualche informazione, sotto).

Tralasciando per il momento tale dato (e anche la logica elementare che serve in alcuni casi) e volendo tirare le somme delle celle SRAM utilizzate in tutti gli altri casi, si arriva a un totale di 50 + 3 + 16 + 6 + 24 + 5 = 99 celle SRAM.

Abbiamo visto nell’articolo che riporta i costi complessi del controllore video dell’Amiga, che questo richiede 384 celle SRAM per l’implementazione di alcuni suoi elementi legati ai bitplane, mentre quello packed ne richiede 248, quindi con un risparmio di 136 celle SRAM. Togliendo le 99 utilizzate sopra, ne rimarrebbero 37, pari a circa 37 x 6 = 222 transistor che rimarrebbero per implementare i 16 mux 4-a-1, cioè quasi 14 transistor a mux. Di nuovo, non essendo del campo e tenendo conto che esistono diverse implementazioni di mux 4-a-1, l’idea che mi sono fatto è che non siamo lontani dal pareggio (ossia che i transistor risparmiati grazie al controllore video packed siano stati “mangiati” dal Blitter packed per questa parte). Un esempio, i merito, è fornito nella pagina su Wikipedia che riporta un’implementazione, la quale richiede 4 port and e 8 porte not, che dovrebbero richiedere 4 x 2 + 8 x 1 = 16 transistor in totale.

Rimane, infine, in piedi la questione dell’uso dei barrel shift (tutti con spostamento massimo di 7 posizioni, quindi con 3 linee di selezione) per gestire il buffer e il byte interno da una parte, e per la concatenazione dei bit rimasti dalla precedente maschera con quelli della nuova che è stata generata. Ne serve uno a 8 bit per shiftare a sinistra il buffer, un altro sempre da 8 bit per ruotare a sinistra il byte interno, e infine un altro da 24 bit per shiftare a destra la nuova maschera che è stata generata e per aggiungerla in coda ai bit rimasti dalla precedente.

La relativa pagina su Wikipedia afferma che per implementare un barrel shifter si utilizzano dei multiplexer (2-a-1), fornendo anche un esempio di barrel shifter a 8 bit in uno dei link esterni. Il problema è che questa soluzione è molto costosa perché anche un semplice mux 2-a-1 richiede un certo numero di porte logiche (e di conseguenza transistor), com’è possible vedere in quest’esempio. Numero che esplode considerando che ne servono 24 per uno a 8 bit e ben 72 per uno a 24 bit (quindi un totale di 2 x 24 + 72 = ben 120 mux 2-a-1 per le nostre esigenze).

In realtà un semplice shifter a 8 bit di una sola posizione, che tra l’altro funziona shiftando sia a sinistra sia a destra (mentre quelli che servono sono monodirezionali), richiede molta meno logica per essere implementato, com’è possibile osservare in quest’altro esempio. Bastano, infatti, 14 porte and, 6 or e un solo inverter (not), quindi 23 porte logiche (approssimativamente perché, come già detto, questo è ciò che serve per uno shifter che funzioni in entrambe le direzioni). Per shiftare fino a 7 posizioni ne servono tre (guardando l’esempio al link esterno di Wikipedia), quindi servirebbero circa 69 porte per un barrel shifter a 8 bit che funzioni in questo modo. Siccome ne servono 5 (2 x 8 bit + 1 x 24 bit), si arriva a circa 345 porte logiche in totale (spannometricamente), che dovrebbero corrispondere approssimativamente a 675 transistor (perché le porte and e or dovrebbero richiedere due transistor, mentre la porta not soltanto uno).

Tirando le somme, il costo per i 3 barrel shifter c’è e sicuramente non è trascurabile in termini di transistor, ma non mi pare esorbitante. Credo, quindi, che fosse abbordabile per i canoni dell’epoca; ricordo che il primo Amiga è stato commercializzato nell’85 e il chip che contiene il Blitter, Agnus, era costituito da ben 21 mila transistor.

Il Blitter – inserimento di un oggetto grafico “mascherato” – AGA

Ci sono poche differenze rispetto all’implementazione di OCS/ECS, in quanto il nuovo algoritmo risulta già di per sé sufficientemente generico da essere facilmente esteso dalla profondità di colore massima di 6 bit (64 colori) fino alla 8 (256 colori) gestibili con l’AGA.

La più importante riguarda senza dubbio il passaggio da mux 5-a-1 a 7-a-1, a causa delle due nuove linee in ingresso che bisogna utilizzare (per poter gestire 128 e 256 colori, rispettivamente). Quindi richiedendo un’implementazione più complessa e che richiede più risorse (transistor).

Un altro elemento, sebbene abbastanza trascurabile, è l’aggiunta di un mux ai 20 già utilizzati per OCS/ECS, perché nel caso di profondità di colore pari a 7 bit è possibile generare maschere di 21 bit.

Infine, il registro interno che memorizza la combinazione dei bit rimasti dalla maschera precedente e di quelli della nuova maschera passa da 24 a 27 bit perché ne servono di più per gestire il caso della profondità colore di 7 bit (in quanto è possibile generare una maschera di 21 bit, a cui si aggiungono i 6 che possono rimanere dalla precedente maschera).

Il costo implementativo cresce, dunque, ma è irrisorio rispetto all’esorbitante numero di celle SRAM richieste per la sola implementazione del controllore video AGA (1280 contro le 444 richieste dell’equivalente packed).

Con questo si chiude l’articolo. Il prossimo tratterà dell’implementazione delle linee in hardware del Blitter e (parzialmente) della modalità di riempimento delle aree.