
Il precedente articolo sul funzionamento del controllore video packed era complesso e decisamente tecnico, per cui ho pensato di presentare un esempio che mostri passo passo il suo funzionamento, in modo da rendere più comprensibile il meccanismo / algoritmo che sta alla sua base.
Il controllore video – packed (OCS/ECS) – Un esempio: come funziona il nuovo controllore video
L’esempio è realizzato in forma tabellare, illustrando lo stato di avanzamento degli slot e delle operazioni interne effettuate, consentendo di vedere come funzionerebbe nella realtà, mostrando anche il caso particolare in cui non ci siano sufficienti dati nel byte interno (“Int. Byte” nella tabella) e di come questa problematica venga risolta in maniera trasparente:
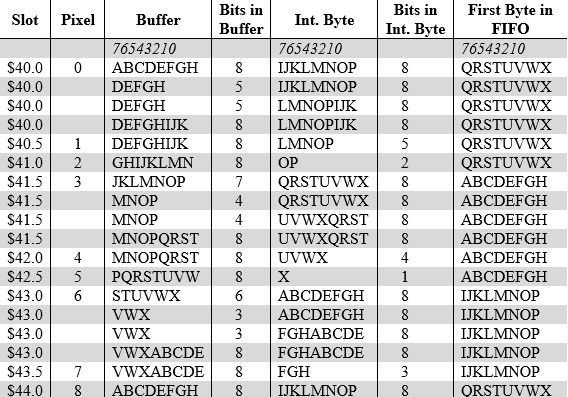
Ho “espanso” il caso del primo pixel (#0) per mostrare le operazioni che vengono effettuate sul buffer, il byte interno, e la coda FIFO (soltanto il primo byte viene mostrato nella colonna “First Byte in FIFO“, il che è sufficiente allo scopo della spiegazione). I letterali presenti in queste tre colonne rappresentano i valori dei singoli bit (per questo, dopo l’intestazione della tabella, è presente una riga coi valori 76543210 in tali colonne, i quali sono figurativamente gli 8 bit in esse contenuti, partendo dal più significativo), ma poiché non c’interessa il loro reale valore, ho preferito nasconderlo usando delle lettere dell’alfabeto (che comunque sono molto utili per capire dove vanno a finire i singoli bit).
La prima riga mostra lo stato iniziale (slot $40.0. Il .0 indica che si tratta del primo ciclo di clock di sistema. Il secondo è indicato come .5), in cui il controllore video si trova nella condizione di dover ottenere l’indice del colore del primo pixel, per cui dal buffer può prelevare immediatamente i tre bit corrispondenti (ABC). Notiamo come inizialmente il buffer sia pieno (8 bit presenti: ABCDEFGH), come pure il byte interno (8 bit anche per lui: IJKLMNOP) e ci sia anche un byte già disponibile nella coda FIFO (QRSTUVWX, che però non verrà mai usato: si dovrà aspettare il processamento del pixel #3); tutto ciò grazie al gestore della coda FIFO, come già descritto in precedenza.
La seconda riga mostra lo stato del buffer (DEFGH) dopo l’eliminazione dei 3 bit estratti: i bit risultano shiftati a sinistra di 3 posizioni, mentre i 3 bit meno significativi sono stati forzati a zero (nella tabella sono rappresentati come spazi vuoti, per evidenziare la mancanza di contenuto). La colonna Bits in Buffer mostra che nel buffer sono presenti adesso soltanto 5 bit, ma si tratta di un’informazione fornita esclusivamente per mostrare come funziona l’idea alla base del nuovo controllore video; infatti non serve sottrarre adesso 3 da 8, per poi nuovamente aggiungere 3 alla quarta riga, perché si calcola tutto in un colpo solo.
La terza riga mostra lo stato del byte interno (LMNOPIJK) dopo essere stato ruotato a sinistra 3 posizioni (cioè il numero di bit necessari al buffer per essere nuovamente pieno), in modo da spostare i suoi 3 bit più significativi (IJK) nei 3 bit meno significativi (quindi esattamente nella posizione in cui serviranno al buffer). Rispetto all’algoritmo presentato in precedenza, la differenza sta nella rotazione a sinistra anziché a destra e nello scorrimento del numero di bit necessari al buffer anziché del numero di bit rimasti nel byte interno; sarà chiaro quando verranno trattati i casi dei pixel #3 e #6.
La quarta riga mostra l’inserimento dei 3 bit meno significativi del byte interno (che adesso sono IJK) nella stessa posizione nel buffer, che adesso risulta nuovamente pieno (infatti il numero di bit in esso contenuti torna a essere 8: DEFGHIJK).
La quinta riga mostra lo stato finale, che corrisponde all’inizio (slot $40.5) del processamento del secondo pixel (#1), dove i 3 bit spostati nel buffer sono stati rimossi (azzerandoli) dal byte interno, con quest’ultimo che adesso conserva soltanto 5 bit (LMNOP, come mostrato nella colonna Bits in Byte Int). Il cerchio si è chiuso…
Lo slot $41.0 relativo al pixel #2 mostra il progressivo svuotamento del byte interno, a favore del buffer (che rimane sempre pieno), ma al momento non c’è nulla di speciale: si va avanti tranquillamente con l’algoritmo appena descritto (e di cui pertanto non serve riportare i progressi delle varie operazioni interne).
Le cose cambiano subito dopo, durante lo slot $41.5 e il processamento del pixel #3. Infatti la fine del processamento del pixel #2 ci ha consegnato uno stato insolito, in quanto il buffer non risulta più pieno (contiene soltanto 7 bit: JKLMNOP), mentre nel byte interno non è rimasto più nessun bit di quelli che aveva inizialmente (IJKLMNOP): gli ultimi due che erano rimasti (OP) si trovano ormai in coda ai bit del buffer. Dunque l’ultima operazione effettuata per il pixel #2 non è stata quella di eliminare i bit dal byte interno (visto che non c’erano più!), ma di rimpiazzarli tutti copiandoli dal primo byte della coda FIFO (QRSTUVWX), la quale adesso ha un altro byte che si trova in testa (ABCDEFGH). Ovviamente il numero di bit del byte interno torna a essere 8.
A questo punto (ossia seconda riga / operazione per il pixel #3) il numero di bit rimasti nel buffer (dopo l’estrazione dei 3 necessari per l’indice colore) non sarà più di 5, com’era avvenuto coi pixel #0 e #1, e #2, ma di 4 (MNOP). Infatti il byte interno sarà ruotato a sinistra di 4 posizioni (UVWXQRST) anziché 3 (terza riga / operazione per il pixel #3). Quindi saranno 4 i bit (QRST) che da esso saranno trasferiti nel buffer (MNOPQRST. Quarta riga / operazione per il pixel #3), e dunque anche 4 quelli rimasti (UVWX. Inizio processamento pixel #4).
Situazione molto simile si presenta all’inizio del processamento del pixel #6 (slot $43.0), dove nel buffer sono rimasti soltanto 6 bit (STUVWX), in quanto il byte interno ha potuto contribuire (durante l’ultima operazione del pixel #5) per un solo bit (X) ed è stato rimpiazzato col primo byte della coda FIFO (ABCDEFGH), che si è quindi spostata al byte successivo (IJKLMNOP). Per cui i bit da copiare diventeranno 5 questa volta (ABCDE) e quelli che rimarranno saranno ovviamente 3 (FGH).
Il processamento dei pixel prosegue poi normalmente, fino al pixel #8, che ci riporta esattamente allo stato iniziale del pixel #0 (ciò perché ho forzatamente inserito nella coda FIFO gli stessi byte, a scopo puramente didattico / esemplificativo). Infatti è anche interessante notare che ogni 8 pixel si ripeteranno esattamente le stesse operazioni (fatto salvo il contenuto dei bit, che ovviamente dipenderanno dalla grafica da visualizzare), e questo banalmente perché, dovendo visualizzare 8 colori e necessitando di 3 bit allo scopo, la grafica risulta perfettamente allineata al byte ogni 3 byte (3 x 8 = 24 bit) processati.
Il controllore video – packed (OCS/ECS) – Costi di implementazione
Passiamo adesso a una stima dell’hardware necessario all’implementazione di quanto è stato esposto finora per il funzionamento “packed” del controllore video.
- Rispetto alla grafica planare serve un solo puntatore (contro ben 6) per i dati dello schermo. Dunque 1 x 2 = 2 registri a 16 bit accessibili dalla CPU, equivalenti a 32 celle SRAM. Servono, pertanto, un sesto delle risorse rispetto all’Amiga (planare).
- I dati prelevati dal “bitplane” finiscono nel buffer (8 bit), nel byte interno (8 bit) e nella coda FIFO (un altro paio di byte). Quindi 4 x 8 = 32 bit pari ad altrettante celle SRAM. 4 bit servono per il contatore del numero del bit nel buffer, altri 4 per il contatore dei bit nel byte interno, ancora 4 per implementare il “puntatore” di testa nella coda FIFO e infine sempre 4 per implementare il “puntatore” di coda; totale: 16 bit AKA celle SRAM. Sostanzialmente tutte queste risorse sono pari a 3 registri dati a 16 bit, mentre all’Amiga ne servono 6 per i registri dati e 6 per i corrispondenti interni, per un totale di 12 registri a 16 bit: il risparmio risulta evidente anche qui (un quarto delle risorse).
- L’indice del colore è sempre disponibile nei bit più significativi, per cui non serve estrarne i singoli bit dai bitplane e combinarli per formare il valore finale, ma serve comunque logica per estrarli dai bit più significativi e azzerare i bit mancanti (per schermi con profondità di colore inferiore a 6 bit per pixel). Penso sia ragionevole assumere che la logica richiesta sia comparabile a quella che fa lo stesso controllore video per la grafica planare.
- Per l’elaborazione di un pixel (a ogni ciclo di clock di sistema) servono 2 barrel shifter a 8 bit con spostamenti fino a 7 posizioni, che sono equivalenti a 2 x 3 barrel shifter a 8 bit da una singola posizione, equivalenti ancora a 3 x barrel shifter a 16 bit da una singola posizione. In questo caso vengono usate metà delle risorse rispetto all’Amiga (6 x barrel shifter a 16 bit da una singola posizione). Serve, però, un po’ di logica per mascherare i bit da copiare i bit dal byte interno al buffer (quindi: generazione di una maschera con bit a 1 dove serve copiare quei bit), e per azzerare i bit copiati nel byte interno (maschera complementare alla precedente), ma si tratta di operazioni binarie molto comuni nonché semplici, per cui penso siano necessari pochi transistor per la loro implementazione (parliamo sempre di dati a 8 bit, per inciso).
- Oltre a quanto sopra, serve altro per implementare correttamente il tutto. Intanto un sommatore/sottrattore a 4 bit per aggiornare il numero di bit rimasti nel buffer dopo l’estrazione dei 3 (nel caso di schermo a 8 colori) per l’indice colore. Un sommatore a 4 bit richiede 4 full-adder, e ogni full-adder richiede 9 transistor per la sua implementazione; dunque sono richiesti un totale di 36 transistor per un full-adder a 4 bit. Serve poi un altro sommatore a 4 bit per calcolare il numero di bit da copiare dal byte interno al buffer. Un altro per sottrarre questo valore dal numero di bit nel byte interno. E un altro per aggiornare il numero di bit nel buffer nel caso in cui i bit copiati dal byte interno non siano sufficienti rispetto a quelli richiesti (vedasi casi per i pixel #3 e #6). In quest’ultimo caso servirà copiare il primo byte della coda FIFO nel byte interno e impostare a 8 il numero di bit in esso disponibili, ma serve poca logica elementare; serve, però, un altro sommatore a 4 bit per far avanzare la testa della coda al prossimo byte disponibile. Alcuni passaggi si potrebbero semplificare, ma ottimizzare al massimo in questo contesto non serve a nulla, considerato che pur nel caso peggiore (l’uso di 5 sommatori a 4 bit) sarebbero necessari 5 x 36 = 180 transistor, quando per implementare un singolo puntatore a bitplane servono 32 x 6 = 192 transistor, mentre sappiamo che il controllore video packed ne ha risparmiati ben 5 (visto che ne serve soltanto uno);
- A ogni caricamento di dati serve incrementare di due (byte) il puntatore (“bitplane“) ai dati dello schermo; quindi serve un sommatore a 32 bit. Ma è soltanto uno, mentre sull’Amiga potrebbero esserne necessari 6 (come discusso in precedenza).
- Per ogni riga da visualizzare è necessario un sommatore da 32 bit per aggiornare il “bitplane” utilizzando il modulo per spostarsi correttamente alla riga successiva. Anche qui ne servono soltanto uno, ma su Amiga potrebbero servirne 6.
Tirando le somme e pur con tutta la complicazione dovuta alla gestione del disallineamento dei dati (per il caso generale dovuto a profondità del colore che non siano potenze del due), il risparmio dell’implementazione packed del controllore video rispetto all’equivalente planare dell’Amiga risulta piuttosto evidente.
Il controllore video – packed (AGA)
Il chipset AGA introdotto con Amiga 4000 e 1200 rappresenta un’evoluzione del precedente ECS, che introduce quali elementi principali l’estensione dei bitplane da 6 a 8 (consentendo, quindi, di visualizzare 256 colori anziché 64. Oppure 262144 colori anziché 4096 nella modalità HAM8), il loro utilizzo a qualunque risoluzione (bassa, alta, super-alta), tavolozza dei colori estesa da 32 a 256 elementi e ognuno di essi presi da 16 milioni invece di 4096, e infine sprite fino a 64 pixel di larghezza (contro i 16 di OCS/ECS). Lascio fuori altre caratteristiche minori, anche perché non sono rilevanti ai fini del confronto packed vs planare.
In ogni caso gli unici elementi degni di attenzione in questo contesto sono gli 8 bitplane e il bus dati che può arrivare a 64 bit.
Passando da 6 a 8 bitplane è stata necessaria l’aggiunta di altri due puntatori per i due nuovi bitplane, e quindi 2 x 2 = 4 registri a 16 bit per la loro implementazione, a cui si devono aggiungere altri 2 registri a 16 bit per i dati letti. Quindi si assiste a un aumento delle risorse richieste (altre celle SRAM da utilizzare allo scopo).
Il pezzo forte, però, è rappresentato dai registri interni utilizzati per i dati letti. Se ne aggiungono altri due ai sei di OCS/ECS arrivando a un totale di 8, ma questa volta tutti questi tipi di registri sono estesi a 64 bit, poiché il controllore video dell’AGA può leggere 64 bit alla volta (anche 32 bit, ma al momento non è importante discuterne) dalla memoria anziché 16 (bit). Risulta, pertanto, evidente che le risorse necessarie allo scopo siano letteralmente esplose (da 6 x 16 celle SRAM siamo passati a 8 x 64: un aumento del 400%).
Col controllore packed, invece, l’aumento risulta decisamente modesto. Infatti è dovuto esclusivamente alla coda FIFO, che anziché ospitare 2 byte ne può (e deve) ospitare 14 (al massimo). Questo perché, per essere sicuro di avere sempre abbastanza dati quando servono, il controllore video richiede sempre un’altra lettura oltre la prima (o precedente). Per cui alla prima lettura leggerà 8 byte, e piazzerà il primo nel buffer, il secondo nel byte interno, e i rimanenti 6 nella coda FIFO. Gli 8 byte della seconda lettura li piazzerà, invece, tutti nella coda (alla sua fine, ovviamente). Quindi nella coda ci saranno al massimo 14 byte a disposizione (che rientra perfettamente nei due registri da 4 bit usati per implementare la testa e la coda, in quanto consentono di esprimere valori da 0 a 15).
Non serve nient’altro, perché il controllore video che deve gestire la grafica packed risulta quasi del tutto svincolato dalla dimensione del bus dati: l’unica cosa che può aumentare è, come abbiamo visto, la dimensione della coda FIFO, che però rimane del tutto trasparente al resto del sistema (è un dettaglio interno).
Tutto ciò mentre il chipset AGA dell’Amiga paga ancora di più il prezzo, visto che gli 8 registri interni sono a 64 bit, e di conseguenza dovrà utilizzare 8 barrel shift a 64 bit (sempre da una posizione), con un aumento anche qui del 400% delle risorse necessarie alla loro implementazione, quando servirà eseguire lo shift per scorrere via via i singoli pixel da visualizzare.
Il controllore video packed rimane, invece, quasi identico, poiché il buffer e il byte interno (che sono gli elementi utilizzati per estrarre gli indici dei colori del pixel) non subiscono nessun cambiamento: questa parte è, diversamente dalla coda FIFO, totalmente disaccoppiata dalla dimensione del bus dati.
Unica differenza è la presenza di un bypass quando la grafica è a 256 colori, perché non è più necessario utilizzare i barrel shifter per il buffer e il byte interno, ma i dati del pixel (un intero byte) vengono immediatamente passati dal secondo al primo (e il primo byte della coda FIFO al secondo). Roba che richiede davvero pochissima logica per essere implementata.
Com’è possibile appurare, il confronto fra controllore planare e packed risulta a dir poco impietoso con l’AGA: esploso col primo mentre estremamente ridotto col secondo. Ma i problemi con l’AGA non finiscono qui, e verranno discussi nella prossima sezione.









