Agli inizi degli anni ’80 le risorse (capacità di elaborazione, frequenza, memoria, archiviazione di massa) a disposizione erano molto scarse, per cui questo periodo è stato caratterizzato dalla sfrenata ricerca di ottimizzazioni nelle applicazioni, qualunque cosa fosse possibile realizzare.
La grafica, come sappiamo, occupa da sempre il posto d’onore in quanto a risorse utilizzate e consumate in un sistema. Scontato, quindi, che si sia cercato di trovare il modo di memorizzarla e utilizzarla in maniera quanto più efficiente possibile per ridurne l’impatto nel sistema, nonostante all’epoca i computer (per lo più “home“) fossero caratterizzati da risoluzioni molto basse (256 e 320 pixel in orizzontale erano quelle più diffuse) e pochi colori (2, 4, … 16 erano già una manna dal cielo!).
Il formato utilizzato per memorizzare le informazioni dei pixel (ossia il colore) era denominato packed (o chunky), e consisteva nell’impiegare un indice numerico (e memorizzarlo in memoria così com’era, in sequenza) a cui corrispondeva poi il colore reale che era conservato a parte in una piccola tabella (tecnicamente chiamata CLUT: Colour Look-Up Table; comunemente chiamata palette o tavolozza dei colori). In un’immagine a 4 colori, ad esempio, gli indici variavano da zero a tre, a cui erano associati quattro colori memorizzati nella CLUT. Un esempio vale più di mille parole:
Dunque un’immagine “packed” era costituita da una sequenza di righe a loro volta formate da sequenze di pixel, il cui colore era memorizzato come indice e il cui spazio occupato dipendeva dal numero di bit necessari a memorizzarlo. Quindi 1 bit era necessario per immagini monocromatiche (2 colori), 2 bit per quelle a 4 colori, ecc. fino a 8 bit per 256 colori (ma si potrebbe continuare, anche se non avrebbe senso: più aumentano i bit e più diventano appetibili i formati senza CLUT, ossia specificando direttamente il colore tramite le sue componenti cromatiche).
Prendendo l’esempio coi 4 colori di cui sopra, i primi 4 pixel erano, quindi, impacchettati (da cui il termine packed) nel primo byte, gli altri 4 pixel nel secondo byte, e così via. Usando, quindi, 2 bit per ogni colore, coi pixel disposti all’interno del byte a seconda dell’endianness del sistema (partendo dai bit bassi per i primi pixel per quelli little-endian, mentre da quelli alti per i sistemi big-endian). Ai fini dell’articolo prenderò come riferimento sistemi little-endian, ma il ragionamento non cambia di una virgola per quelli big-endian.
Il formato per memorizzare la grafica planare (planar graphic) si differenzia, invece, da quello packed per il fatto di distribuire su piani (zone di memoria) diversi i vari bit degli indici dei colori; da cui il nome bitplane. Un’altra immagine, questa volta per grafica a 16 colori, consente di comprendere meglio il concetto:
Dunque per immagini a 4 colori (che utilizzano 2 bit per i relativi indici) la grafica sarà memorizzata in due bitplane: il primo che conterrà tutti i bit 0 (primo bit) degli indici colore, mentre il secondo conterrà tutti i bit 1 (secondo bit) dei medesimi indici. Per 16 colori serviranno, invece, 4 bitplane; e così via.
A prima vista sembra una complicazione (e per lo più lo è, infatti, come vedremo), visto che più aumentano i colori e di più bitplane avremo bisogno in cui distribuire tutti i dati nonché per accedervi quando ci interessino determinati pixel, mentre con la grafica packed tutti i dati di un singolo pixel si trovano nello stesso posto.
La grafica planare dovrebbe, quindi, presentare delle caratteristiche peculiari e vantaggiose rispetto a quella packed, che l’avranno fatta preferire a quest’ultima. Una leggenda metropolitana, piuttosto diffusa e assurta a verità, li vorrebbe più efficienti in termini di spazio occupato o di complicazione circuitale nei confronti di quella packed quando ci si trovi in presenza di un numero di colori che non siano potenze di due (quindi 8, 32, 64, e 128 colori, pari a 3, 5, 6, e 7 bit utilizzati; questo per citare le più comuni).
Ciò sembra essere la motivazione principale che abbia portato Jay Miner a implementare la grafica dell’Amiga in formato planare anziché packed, e ancora oggi viene comunemente propugnata e sbandierata da diversi amighisti come il vantaggio che questa macchina ebbe nei confronti delle macchine concorrenti (Atari ST, PC, Mac, ecc., incluse le console).
Inutile dire che se ho scritto quest’articolo è proprio per mettere definitivamente fine a questa falsità che per troppo tempo ha, purtroppo, alimentato e diffuso un concetto del tutto sbagliato. Infatti la grafica packed risulta quasi sempre più efficiente di quella planare, qualunque sia il numero di colori e la configurazione hardware del sistema (ampiezza del bus dati), fatta eccezione per alcuni casi decisamente meno frequenti (come per esempio l’accesso a uno o pochi bitplane rispetto alla totalità = profondità del colore = numero di bit necessari per rappresentare i colori).
Per semplicità mostrerò alcuni dati squisitamente numerici relativi a configurazioni dotate di bus dati a 8 (in particolare), 16, e 32 bit, per cercare di semplificare la trattazione, ma chiaramente il discorso si estende anche a sistemi con bus più ampi.
Parto subito dal controllore video, che si occupa di leggere dalla memoria video (o di sistema, nel caso di una piattaforma in cui la memoria sia condivisa da tutti i dispositivi) i dati della grafica da visualizzare, riga per riga, prelevando gli indici dei colori dei pixel, convertendoli nel colore vero e proprio (usando la CLUT), per poi spedirlo al monitor per essere finalmente mostrato all’utente.
Sempre per non appesantire il pezzo, assumerò sempre che lo schermo e la grafica utilizzino 8 colori (quindi saranno necessari 3 bit per memorizzarne l’indice), ma lo stesso identico ragionamento può essere tranquillamente applicato a grafica con qualunque altra profondità di colore, perché valgono esattamente le medesime analisi, considerazioni, e risultati simili.
Con un bus dati a 8 bit una riga della grafica packed avrebbe la seguente configurazione in memoria:
mentre con quella planare (maggiori dettagli sotto, quando parlo del formato Amiga):
Nel caso di grafica packed il controllore video leggerà un byte alla volta dalla memoria, estrarrà i 3 bit di un pixel (operazione di mascheramento: effettuata con un semplice and binario col valore 7 decimale = 111 in binario, che restituisce immediatamente il valore dell’indice), utilizzerà quindi l’indice per leggere il colore vero e proprio dalla CLUT, lo manderà al monitor, e infine eseguirà uno shift a destra di 3 per eliminare il pixel attuale ed essere pronto col successivo.
Nel caso in cui il byte rimasto non possedesse sufficienti bit per ricavare l’indice del prossimo pixel (ad esempio per il terzo pixel visualizzato mancherebbe un bit per completare l’indice colore), il controllore leggerà un altro byte dalla memoria, ne eseguirà un opportuno shift e lo concatenerà (con un or binario) a ciò che era rimasto; in tal modo potrà proseguire con la visualizzazione del successivo pixel.
Con la grafica planare la situazione si fa più complicata, perché i dati dei pixel sono sparsi su 3 diversi bitplane. Ma non solo: esistono anche tre modi diversi di memorizzare la grafica.
Il primo, ad esempio usato dall’Atari ST, memorizza i bitplane in sequenza (16 pixel alla volta nel caso dell’ST, a causa del bus dati a 16 bit). Quindi in un sistema con bus dati a 8 bit il primo byte rappresenterebbe il primo byte del bitplane 0, il secondo byte sarebbe il primo del bitplane 1, e infine il terzo byte sempre il primo del bitplane 2. Per poi ripetersi nuovamente ripartendo dal secondo byte del bitplane 0:
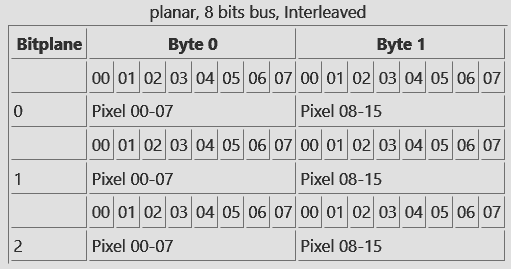
Nel secondo modo i dati dei bitplane sono distribuiti una riga alla volta. Quindi prima si trovano i byte di tutta la prima riga del bitplane 0, poi quelli della prima riga del bitplane 1, e infine quelli del bitplane 2. Si ricomincia poi coi dati della seconda riga del bitplane 0, e così via. Questa modalità è anche chiamata “interleaved“:
Il terzo modo (già mostrato prima) è quello usato dall’Amiga (che comunque, data la libertà del controllore grafico e, parzialmente, del Blitter, può implementare / usare anche il formato interleaved) che risulta essere anche il più flessibile, in quanto i dati dei bitplane sono tutti memorizzati in maniera contigua. Inoltre possono stare in qualunque locazione di memoria. L’ulteriore prezzo da pagare è, però, la necessità di utilizzare 3 diversi puntatori per andare a leggere i dati (visto che possono essere in tre di zone di memoria completamente diverse): uno per ogni bitplane.
A prescindere dal formato con cui sono memorizzati i dati dei bitplane, il controllore video avrà bisogno di leggere 3 byte, uno per ogni bitplane, prima di poter iniziare a visualizzare i pixel. Dunque servono 3 buffer interni in cui memorizzare i suddetti byte. Una volta letti i 3 byte, provvederà a estrarre il primo bit di ognuno di essi, effettuare un opportuno shift a sinistra dei bit estratti (nessuno per il bitplane 0; uno shift per il bitplane 1; due shift per il bitplane 2), e combinarli (con un’operazione di or binario) per ottenere finalmente l’indice del colore. A questo punto potrà usare l’indice per leggere il colore vero e proprio dalla CLUT, mandarlo al monitor, e infine eseguire uno shift a destra di tutti e tre i byte per eliminare il pixel attuale ed essere pronto col successivo.
Nel caso in cui i byte rimasti non abbiano più alcun bit per ricavare l’indice del prossimo pixel (perché sono stati visualizzati tutti e gli 8 pixel), il controllore leggerà altri tre byte dalla memoria (a seconda del formato implementato per i bitplane); in tal modo potrà proseguire con la visualizzazione del successivo pixel.
Risulta già evidente come, contrariamente alle aspettative, la semplice operazione di visualizzazione di grafica planare richieda più risorse (più buffer) e una circuiteria più complicata rispetto a quella packed. Inoltre è bene sottolineare che, dovendo leggere più byte in memoria prima di poter iniziare a lavorare, il controllore video inizierà più tardi nel visualizzare i pixel, aggiungendo, quindi, una certa latenza (cioè il tempo che passa da quando il primo dato inizia a essere letto dalla memoria a quando il primo pixel verrà effettivamente visualizzato sullo schermo).
Per quanto riguarda lo spazio occupato (che si riflette anche sul numero di accessi alla memoria e, dunque, sulla banda di memoria necessaria) e supponendo di avere uno schermo con una risoluzione orizzontale di 256 pixel, una riga richiederà 256 * 3 = 768 bit = 96 byte in memoria che dovranno essere letti (sequenzialmente) per visualizzare la grafica packed. Per la grafica planare il risultato è lo stesso (perché ci saranno 3 righe da 256 bit = 32 byte ciascuna). Questo perché la risoluzione orizzontale è un particolare multiplo di 8, e quindi non ci sono differenze.
Similmente, con una risoluzione di 320 pixel, invece, abbiamo 320 * 3 = 960 bit = 120 byte per la grafica packed, e 40 byte per ognuno dei tre bitplane per quella planare.
I problemi e le differenze emergono ovviamente quando la risoluzione orizzontale non risulti più un multiplo di 8. Prendendo una risoluzione base di 256 pixel orizzontali, i casi peggiore, medio, e migliore sono rappresentati da 1, 4 o 7 pixel in più; quindi risoluzioni di 257, 260, e 263 pixel.
Nel primo caso una riga richiederà 257 * 3 = 771 bit = 96,375 byte in memoria che dovranno essere letti (sequenzialmente) per visualizzare la grafica packed. Arrotondando, serviranno 97 byte per riga, con uno spreco di poco più di mezzo byte.
Nel secondo caso richiederà 260 * 3 = 780 bit = 97,5 byte in memoria che dovranno essere letti (sequenzialmente) per visualizzare la grafica packed. Arrotondando, serviranno 98 byte per riga, con uno spreco di mezzo byte.
Infine nel secondo caso richiederà 263 * 3 = 789 bit = 98,625 byte in memoria che dovranno essere letti (sequenzialmente) per visualizzare la grafica packed. Arrotondando, serviranno 99 byte per riga, con uno spreco di poco meno di mezzo byte.
Per la grafica planare i risultati cambiano a seconda del formato utilizzato per memorizzare i dati dei bitplane.
Intanto i calcoli per singola riga di un bitplane sono i seguenti: 257 pixel = 32,125 byte in memoria; arrotondando, serviranno 33 byte per riga (per bitplane), con uno spreco di più di mezzo byte. 260 pixel = 32,5 byte; arrotondando, serviranno 33 byte per riga, con uno spreco di mezzo byte. Infine, 263 pixel = 32,875 byte; arrotondando, serviranno sempre 33 byte per riga, con uno spreco di poco meno mezzo byte.
Nel formato “Atari ST” si avrebbe lo stesso spreco delle rispettive packed, se i dati (i tre bit necessari per memorizzare l’indice del colore) dell’ultimo pixel fossero impacchettati tutti assieme (nello stesso byte). Ma questo complicherebbe notevolmente il controllore video, perché dovrebbe prevedere una diversa modalità di funzionamento per gli ultimi pixel dello schermo da visualizzare (quelli accorpati nel singolo byte). Senza questa complicazione sarebbe, invece, necessario utilizzare un byte extra per ogni bitplane, triplicando lo spreco rispetto alla grafica packed.
Un ragionamento simile si può fare col formato “interleaved” e con quello “Amiga”: accorpare i bit rimanenti, in questo caso, significherebbe unire le righe, una di seguito all’altra.
Nel caso della “interleaved” ciò vorrebbe dire che alla fine dei bit del bitplane 0 si troveranno immediatamente impacchettati i bit del bitplane 1, e lo stesso alla fine del bitplane 1 con quelli del bitplane 2. E’ facile intuire quanto ciò complicherebbe enormemente il lavoro del controllore video, che si troverebbe a dover eseguire shift e mascheramenti per separare i dati dei vari bitplane a inizio (o fine) di ogni riga.
Stesso discorso per il formato “Amiga”, anche se in questo caso ci sarebbe il vantaggio che fine e inizio di ogni riga sarebbero relativi allo stesso bitplane. I limiti e la complessità, comunque, rimangono.
Numeri e calcoli mostrano come indubitabilmente la grafica packed sia quella a richiedere meno complessità circuitale nonché miglior efficienza, con uno spreco nell’ordine del singolo byte (per riga), e questo a prescindere dal numero di colori visualizzati (fino al limite di 256 = 8 bit, ovviamente).
Questo è un dato di particolare importanza, perché gli sprechi aumentano, invece, per la grafica planare, in misura lineare rispetto ai bit necessari per il numero di colori da visualizzare. Dunque se per 8 colori si assiste a uno spreco di 3 byte, con 128 colori lo spreco arriva a ben 7 byte. Che moltiplicato per il numero di righe fa certamente sentire il suo peso.
Se pensaste che gli esempi fatti con risoluzioni orizzontali “strane” come 257, 260, e 263 pixel fossero inutili e quindi un puro esercizio di stile, tornereste sui vostri passi nel momento in cui comincereste a rendervi conto di come effettuare lo scorrimento (scrolling) in orizzontale di uno schermo visualizzato, come avveniva spesso in diversi giochi o con applicazioni che mostravano una porzione di uno schermo fisicamente più grande.
In questi casi eseguire lo scroll a destra (ad esempio) di un pixel di uno schermo da 256 pixel orizzontali significa sostanzialmente dover prelevare i dati di 257 pixel, scartandone il primo. Allo stesso modo, lo scroll a destra di 7 pixel equivale a prelevare i dati sempre di 263 pixel, ma scartando i primi 7 questa volta. Solo che scartare pixel è un’operazione molto più efficiente per la grafica packed, perché servirà sempre e comunque leggere un solo byte extra, mentre per quella planare se ne dovranno leggere sempre 3 (e così via per quando aumenta la profondità del colore).
Tutto torna…
Ritornando a parlare di efficienza e sprechi, i suddetti numeri aumentano proporzionalmente con l’aumentare della dimensione del bus dati. Quindi passando da 8 a 16 bit gli scenari di cui sopra portano a sprechi di 2 byte o di 6 byte massimi per riga, rispettivamente per la grafica packed e quella planare (sempre considerando 8 colori = 3 bit per pixel). Da 16 a 32 bit gli sprechi passano a 4 e 24 byte. E così via con dimensioni di bus più ampie e/o con l’obbligo di eseguire accessi in modalità “burst” alla memoria. Dunque più aumenta la dimensione del bus dati e più aumenta lo spreco di spazio utilizzando risoluzioni non perfettamente a esso allineate.
Conclusa la trattazione relativa al controllore grafico (che comunque è molto importante per comprendere il resto, poiché le problematiche relative ai disallineamenti sono le medesime) passo a quella relativa all’implementazione di alcune primitive grafiche comunemente utilizzate per manipolare la grafica. Di seguito, per semplificare la trattazione, ometterò il calcolo della (o delle) locazione di memoria a cui accedere nei vari casi in esame.
Le più semplici sono ovviamente quelle di lettura e scrittura del colore (indice, in questo caso) di un pixel.
Nel caso di grafica packed sono alquanto banali e immediate.
Per la lettura sarà sufficiente leggere il byte in cui trovano i 3 bit che conservano il valore dell’indice, effettuare un opportuno shift a destra se il primo di tali bit non si trovi esattamente nella prima posizione (LSB), e infine mascherarli (eseguendo un and binario col valore 7 decimale = 111 in binario).
Per la scrittura l’operazione richiede la lettura del byte, mascherando immediatamente i 3 bit che dovranno essere sostituiti, eseguendo un opportuno shift a sinistra per posizionare i 3 bit del nuovo indice da scrivere, eseguendo l’or binario fra il byte mascherato e l’indice shiftato, e infine scrivendo il risultato nel byte in memoria.
Questo nel caso migliore in cui i 3 bit dell’indice da leggere o scrivere si trovino tutti nello stesso byte. In caso diverso sarà, invece, necessario leggere i due byte adiacenti, ma poi si procederà esattamente allo stesso modo.
Questo significa che, prendendo 3 byte alla volta (perché ogni 3 byte si ripete esattamente la stessa configurazione di pixel, in uno schermo a 8 colori, come mostrato nella relativa immagine all’inizio dell’articolo), i casi migliori sono quelli relativi ai pixel #0, 1, 3, 4, 6, 7. Mentre i casi peggiori si hanno coi pixel #2 e 5. Questo vuol dire che il caso migliore si presenterà nel 6/8 = 75% dei casi (lettura/scrittura di un solo byte, per un totale di 2 accessi alla memoria), mentre il caso peggiore nel rimanente 2/8 = 25% (lettura/scrittura di due byte, per un totale di 4 accessi alla memoria).
Passando a un bus dati a 16 bit la situazione migliora nettamente. Infatti i casi migliori sono relativi ai pixel #0..4, 6..9, 11..15, mentre quelli peggiori riguardano i pixel #5 e 10; il che è naturale, visto che ci saranno sempre e soltanto due casi (all’interno della sequenza che si ripete ogni 3 volte la dimensione del bus dati) di pixel che si accavallino in due locazioni differenti (e attigue). Quindi il caso migliore si verificherà nel 14/16 = 87,5% dei casi, e quello peggiore nel rimanente 2/16 = 12,5%.
Inutile dire che passando a bus dati di dimensioni maggiori i casi migliori aumenteranno ancora, mentre diminuiranno quelli peggiori. Possiamo quindi dire che, in generale, più aumenta la dimensione del bus dati e più rari saranno i casi peggiori, in quanto ci saranno sempre e soltanto due pixel il cui indice sarà memorizzato in due byte contigui anziché in uno soltanto.
Passando alla grafica planare, la situazione è più semplice poiché non ci sono casi migliori o peggiori da considerare, in quanto tutto è relativo al numero di bitplane da leggere e/o scrivere ogni volta: sono loro, e soltanto loro, che condizionano il numero di operazioni verso la memoria per le primitive di lettura o scrittura di un pixel.
Ciò vale a prescindere dal formato planare utilizzato (Atari ST, interleaved, o Amiga), poiché le uniche differenze nei tre casi sono relative al calcolo della posizione del byte interessato. Il quale sarà un offset fisso di 0, 1 e 2 byte (per indirizzare i dati del primo, secondo, o terzo bitplane) per quello Atari ST; un offset dinamico di 0, 1 * lunghezza riga, e 2 * lunghezza riga per l’interleaved; e, infine, si dovranno utilizzare tre diversi puntatori per il formato Amiga. Queste differenze saranno sempre le stesse, qualunque sia la primitiva grafica, e quindi non saranno più considerate da qui in avanti.
La lettura è l’operazione più semplice, poiché basta leggere i byte dei tre bitplane, mascherare (con un and binario) il bit interessato, eseguire un opportuno shift per posizionarli rispettivamente al primo, secondo, e terzo bit, e infine combinarli (con un or binario) per ricostruire l’indice del pixel interessato. Sono, quindi, necessarie tre operazioni di lettura in memoria.
La scrittura si complica perché è necessario estrarre i tre bit, uno per ogni bitplane che dev’essere scritto, con operazioni di mascheramento, shiftarli in modo da sistemarli nella posizione in cui devono essere scritti all’interno dei tre byte dei rispettivi bitplane, poi leggere tali byte, togliere di mezzo (di nuovo, con operazione di mascheramento = and binario) l’attuale valore, combinarli (con or binario) coi bit precedentemente estratti, e infine scrivere i 3 byte nelle locazioni di memoria dei rispettivi bitplane. Sono, quindi, necessarie tre operazioni di lettura in memoria e tre di scrittura, per un totale di 6 accessi.
Risulta piuttosto evidente come la grafica packed richieda non soltanto meno operazioni di lettura e scrittura in memoria, ma pure molte meno operazioni per portare a termine le primitive. La grafica planare è indubitabilmente più onerosa da tutti i punti di vita e, dunque, più inefficiente, sia in termini di banda di memoria richiesta sia in termini puramente computazionali (per l’implementazione delle due primitive grafiche).
Si potrebbe pensare che questo sia un caso particolare che risulti troppo indigesto alla grafica planare ma, sebbene le operazioni di lettura e scrittura dei pixel siano effettivamente le peggiori in assoluto, queste primitive basilari in ogni caso rappresentano lo specchio della situazione che si viene a creare adottando questo formato grafico. Con altre primitive gli effetti sono più ridotti (perché è possibile operare su più pixel alla volta, mitigando le suddette problematiche), ma in ogni caso non spariscono del tutto né risulteranno vantaggiose (se non in pochi scenari) rispetto alle controparti packed.
Disegnare linee, infatti, mette ancora una volta in risalto le stesse problematiche, e questo perché in genere questa primitiva viene implementata disegnando un pixel alla volta. Gli unici casi in cui si potrebbe ottimizzare si verificano quando ci sono due o più pixel adiacenti e orizzontali appartenenti alla linea che si deve tracciare. Il caso migliore è ovviamente rappresentato dal disegno di una linea orizzontale, dove tutti i pixel sono adiacenti e risiedono tutti sulla medesima riga, per l’appunto.
Prendendo il caso migliore (i casi medi per tutte le primitive grafiche sono poco interessanti, poiché le analisi e valutazioni ricadono tutte “in mezzo” ai casi migliori e peggiori, per cui non li tratterò) e, in particolare, il tracciamento di una linea orizzontale di due pixel, con la grafica packed esistono tre possibili scenari (ricordando sempre che stiamo parlando di grafica a 8 colori = 3 bit necessari per memorizzare l’indice del colore del pixel).
Il primo si verifica quando i due pixel appartengono entrambi allo stesso byte, per cui sono necessarie una sola lettura e una sola scrittura per completare l’operazione, per un totale di 2 accessi in memoria. Questo tralasciando operazioni di mascheramento (and binario), shift, e inserimento (or binario) dei valori, che sono sostanzialmente comuni a qualunque formato utilizzato, e che da qui in poi non verranno più considerate nelle analisi (è sufficiente far riferimento a quanto già esposto parlando di lettura e scrittura dei singoli pixel). Il numero di operazioni di lettura e scrittura in memoria è il fattore più importante parlando di primitive grafiche (lasciando perdere roba come shader et similia), ed è quindi su questo che mi concentrerò per valutare l’efficienza di un sistema grafico packed o planare.
Il secondo caso è rappresentato dal primo pixel che risiede in un byte e il secondo che, invece, si trova nel byte successivo. Il terzo caso è molto simile a questo, e si verifica quando uno dei due pixel sta interamente in un byte, mentre il secondo sta parzialmente nello stesso byte e la parte rimante nel byte attiguo. Entrambi si possono accorpare, perché risulta evidente che le operazioni di lettura e scrittura sono sempre due in entrambi i casi, per un totale di 4 accessi alla memoria.
Passando alla grafica planare, gli scenari possibili sono sempre due. Il primo (che è anche il migliore) si verifica quando entrambi i pixel si trovino nello stesso byte (dello stesso bitplane). In questo caso è banale verificare che per tracciarli siano necessarie tre operazioni di lettura e tre di scrittura, per un totale di 6 accessi alla memoria.
Il secondo caso è chiaro che si abbia quando i due pixel non risiedano nello stesso byte, per cui il primo pixel dovrà essere scritto in un byte, mentre il secondo in un altro (non necessariamente il successivo: dipende dallo specifico formato planare utilizzato dei tre). Le operazioni di lettura e scrittura risultano quindi raddoppiate, passando a 6 + 6 = 12 accessi alla memoria.
Il confronto risulta impietoso e indubbiamente a favore della grafica packed, ma c’è da dire che quello della linea orizzontale con due soli pixel tracciati risulti rispettivamente il caso migliore per la grafica packed e il peggiore per quella planare. Infatti all’aumentare della lunghezza della linea orizzontale (fino a un massimo di 8 pixel, visto che stiamo parlando di sistemi con bus dati a 8 bit; oltre gli 8 bit = dimensione del bus poi il ragionamento si ripete ciclicamente) i casi peggiore e migliore della grafica planare rimangono esattamente gli stessi, ma cambiano per la grafica packed, che vede aumentare il numero di accessi alla memoria.
Prendendo il caso di 3 pixel da tracciare, si può verificare facilmente che il caso migliore e peggiore coincidano con la grafica packed, poiché verrà sempre richiesto di leggere e scrivere due byte (pari a 4 accessi alla memoria, dunque).
Con 4 pixel abbiamo il caso migliore che richiede sempre 2 + 2 = 4 accessi, mentre quello peggiore ne richiede 3 + 3 = 6 accessi (abbiamo raggiunto il caso migliore della grafica planare). La stessa cosa si verifica con 5 pixel da disegnare.
La situazione cambia con 6 pixel da tracciare, perché il caso migliore passa a 3 + 3 = 6 accessi, mentre quello peggiore (che comunque è il più raro: si verifica una sola volta su 8 possibilità) a 4 + 4 = 8 accessi. Idem con 7 pixel, ma questa volta i casi peggiori si verificano su 4 casi su 8. E infine con 8 pixel da disegnare il caso migliore si verifica soltanto una volta su 8.
Com’è possibile vedere, esistono dei casi in cui la grafica planare richieda meno accessi (6) rispetto a quella packed (8), ma il numero di scenari in cui ciò si verifichi risulta in ogni caso nettamente minore rispetto quelli in cui quella packed fa meglio. Inoltre è bene sottolineare che si sta confrontando il caso migliore per la grafica planare con quello peggiore di quella packed, mentre il caso peggiore di quella planare (12 accessi) è nettamente distanziato da quello peggiore della packed (sempre 8).
Infine, e come già evidenziato con le primitive sui singoli pixel, più aumenta la dimensione del bus dati e più rari diventano i casi peggiori per la grafica packed (si riducono i casi di sovrapposizioni di locazioni di memoria adiacenti), per cui il vantaggio incrementa ancora di più.
La trattazione estensiva sui casi relativi alle linee orizzontali (nonché quella precedente sui singoli pixel) non è frutto di puro esercizio, ma si è resa necessaria perché rappresenta la base per qualunque altra primitiva, e dunque valgono esattamente le stesse considerazioni (ma “moltiplicate” per il numero di linee orizzontali che saranno interessate negli specifici casi).
Un naturale esempio è rappresentato dal tracciamento di un rettangolo, essendo costituito da un certo numero di linee orizzontali (tutte della medesima lunghezza). Ma anche un cerchio altro non è che un insieme di linee orizzontali di lunghezza variabile. E così via per primitive più complesse, che si possono sempre scomporre in un insieme di linee orizzontali da tracciare.
Tuttavia una menzione speciale meritano le primitive cosiddette di “bit-blitting“, e in particolare quelle di copia di una porzione rettangolare (di uno schermo / framebuffer), spostamento di una porzione rettangolare, e di inserimento di un oggetto grafico “mascherato“ (ad esempio visualizzazione di uno “sprite” sullo schermo, tenendo conto dei “buchi” dello sprite che lasciano visualizzare la grafica dello schermo anziché la sua. Nel gergo amighista questo tipo di operazione viene chiamata “cookie-cut“).
Premesso che anche in questi casi valgono le medesime considerazioni di cui sopra, queste primitive sono particolarmente importanti perché sono le più usate nei videogiochi (disegnare gli schermi usando delle “mattonelle” = tile in gergo, ripristinare lo sfondo sporcato, disegnare gli sprite, ecc.) o dai gestori delle interfacce grafiche (per spostare finestre, disegnare immagini, ecc.) nonché quelle più pesanti (in termini di utilizzo della memoria). Per tale motivo sono nati anche appositi acceleratori hardware, che sono stati chiamati Blitter.
Poiché le primitive di bit-blitting operano tutte su porzioni rettangolari, mi limiterò a trattare (velocemente perché, come già detto, valgono in ogni caso le stesse considerazioni effettuate nel caso del disegno di linee orizzontali) le operazioni su singola riga, considerato che per tutte le righe è sufficiente ripetere la stessa analisi per poi tirare le somme.
Copiare una porzione rettangolare di schermo (o, in generale, di un framebuffer) significa che il rettangolo può essere locato in qualunque parte di esso, mentre la copia risiederà in un buffer allineato alla dimensione del bus dati (come minimo). In soldoni vuol dire che si può copiare un rettangolo di pixel a partire da qualunque posizione orizzontale (0, 1, 2, 3, ecc.) di una sua riga, ma il primo pixel di tale rettangolo verrà copiato sempre a partire dal primo bit del primo byte della locazione di memoria che funge da buffer di memorizzazione per la grafica.
Copiare un rettangolo di ampiezza pari a un solo pixel è banale e ricade nella lettura e poi scrittura del singolo pixel, che è già stato trattato.
Con ampiezza di due pixel e per quanto riguarda la grafica packed i casi possibili sono due: i due pixel risiedono nello stesso byte, oppure in due byte attigui. Nel primo caso (migliore) la copia richiederà 2 letture dalla memoria (ricordiamo sempre che lo schermo è a 8 colori = 3 bit usati per l’indice dei colori) per estrarre gli indici dei colori e poi una sola scrittura nel buffer; 1 + 1 = 2 accessi in memoria. Nel secondo caso (peggiore) le operazioni di lettura ovviamente raddoppiano, ma si mantiene quella di scrittura; quindi alla fine avremo 2 + 1 = 3 accessi in memoria. Quindi si va da un minimo di 2 accessi a un massimo 3.
Con la grafica planare il ragionamento è esattamente lo stesso, perché sussistono gli stessi scenari migliore e peggiore. La differenza è che nel primo caso (migliore) la copia richiederà 3 letture dalla memoria e poi 3 scritture nei bitplane del buffer; quindi 3 + 3 = 6 accessi in memoria. Nel secondo caso (peggiore) le operazioni di lettura raddoppiano (come per la grafica packed), per cui gli accessi saranno 6 + 3 = 9. Quindi si va da un minimo di 6 accessi a un massimo 9.
Anche qui, sembra che la grafica packed risulti enormemente più efficiente di quella planare, ma la situazione migliora leggermente per quest’ultima aumentando l’ampiezza dei rettangoli, riproponendo alcuni scenari in cui risulta migliore della prima. Si tratta, comunque, sempre di pochi casi rispetto alla totalità degli scenari. Non rifarò nuovamente analisi e calcoli per ampiezze maggiori di due pixel, per non appesantire troppo la trattazione (visto che l’articolo ha già raggiunto una notevole lunghezza).
Lo spostamento di una porzione rettangolare è molto simile alla primitiva di copia, ma con due differenze. Intanto non c’è un buffer in cui copiare la grafica allineata, perché la copia avviene su una qualunque altra porzione rettangolare dello schermo (di destinazione; che potrebbe anche coincidere con quello di origine); dunque la scrittura del primo pixel del rettangolo originale può finire su qualunque altro pixel della destinazione (leggi: la scrittura può essere non allineata alla dimensione del bus dati). Inoltre bisogna preservare la grafica esistente nello schermo di destinazione (nel caso della copia, invece, i bit non coinvolti venivano lasciati a zero).
Rimanendo per semplicità sempre al caso del rettangolo con ampiezza di due pixel, è chiaro che le stesse considerazioni effettuate durante la copia dallo schermo sorgente valgono ancora per quello di destinazione. Dunque esistono i classici due casi, migliore e peggiore, in cui i due pixel di destinazione risiedano nello stesso byte o in due byte adiacenti. Questo significa che saranno necessarie una o due operazioni di lettura, a cui si aggiungono le rispettivamente una o due operazioni di scrittura in memoria. La combinazione dei due scenari per l’origine e i due per la destinazione porta a ben quattro casi, che spaziano da entrambi i casi migliori fino a entrambi quelli peggiori.
Questo perché, con la primitiva di spostamento, non soltanto bisogna estrarre i due pixel dalla porzione rettangolare di origine, ma poi tali pixel devono anche essere inseriti opportunamente nella regione di destinazione. Per cui sarà necessario mascherare opportunamente i byte interessati in tale regione (in modo da non alterare i bit dei pixel non coinvolti dall’operazione e che si trovino adiacenti ai lati dei due da cambiare), per poi combinarli coi valori degli indici dei due pixel letti, e infine memorizzare il risultato.
Nel caso della grafica packed, per entrambi i casi migliori avremo bisogno di 1 + 1 = 2 letture e una scrittura; quindi un totale di 3 accessi alla memoria. Per i casi peggiori avremo, invece, bisogno di 2 + 2 = 4 letture e due scritture; per un totale di 6 accessi. Nei due casi intermedi avremo, invece, 2 + 1 + 1 = 4 accessi, e 1 + 2 + 2 = 5 accessi. Quindi si va da un minimo di 3 accessi a un massimo di 6.
Ragionamento analogo per la grafica planare. Per entrambi i casi migliori abbiamo bisogno di 3 + 3 = 6 letture e 3 scritture; quindi 9 accessi in memoria. Per entrambi i casi peggiori, invece, serviranno 6 + 6 = 12 letture e 6 scritture, per un totale di 18 accessi. Nei casi intermedi, infine, abbiamo rispettivamente 6 + 3 + 3 = 12 accessi, e 3 + 6 + 6 = 15 accessi. Quindi si va da un minimo di 9 accessi a un massimo di 18.
Ancora una volta, aumentando l’ampiezza dei rettangoli (più pixel orizzontali da spostare) la grafica planare migliora un po’, e in alcuni (pochi) scenari risulta leggermente più efficiente, ma complessivamente l’efficienza è di gran lunga migliore per la grafica packed.
Ultima primitiva di bit-blitting è quella di inserimento di un oggetto grafico “mascherato”. Questa è molto simile alla precedente primitiva di spostamento di una porzione rettangolare, con la differenza che viene utilizzata anche una “maschera”, ossia un altro oggetto grafico monocromatico (quindi un bitplane) che consente di stabilire se nella destinazione dev’essere copiato il pixel della sorgente o mantenuto quello della destinazione.
A livello di calcoli valgono, quindi, esattamente le stesse considerazioni, a cui va aggiunto, però, il numero di accessi alla memoria necessari alla lettura dei byte della maschera.
Sempre tenendo conto di rettangoli di ampiezza di due pixel, una maschera potrebbe averli memorizzati in due byte attigui, e quindi le operazioni di lettura sarebbero una nel caso migliore e due in quello peggiore.
Questo significa che i quattro scenari illustrati precedentemente per la grafica packed risultano raddoppiati tenendo conto degli altri due portati in dote dalla gestione della maschera. Sarà, quindi, sufficiente aggiungere uno o due byte ai quattro casi precedentemente esaminati, per ricavare il numero totale di accessi alla memoria richiesti per implementare questa primitiva. Quindi si va da un minimo di 4 accessi a un massimo di 8.
Con la grafica planare il ragionamento è simile, ma con la differenza sostanziale che la lettura della maschera è richiesta per ogni singolo bitplane a cui applicare l’operazione di inserimento con maschera. Questo perché, per l’appunto, i bitplane sono separati, e dunque ogni volta che si finisce col processare un bitplane poi bisogna nuovamente ricaricare la maschera e ricominciare dall’inizio quando si opererà con un altro.
Con tale formato grafico, dunque, ai dati sugli accessi dei quattro scenari relativi allo spostamento vanno aggiunti 3 o 6 byte per la lettura della maschera. Quindi si va da un minimo di 12 accessi a un massimo di 24.
Come si può vedere, per quest’ultima primitiva analizzata il formato planare risulta ancora più penalizzato rispetto a quello packed, perché più aumentano i bitplane e proporzionalmente più aumentano gli accessi per leggere sempre la stessa maschera: uno spreco enorme considerato che la maschera è sempre la stessa.
Dulcis in fundo, col formato packed è possibile pensare di calcolare automaticamente la maschera partendo dal valore dell’indice dell’oggetto grafico sorgente, usando, ad esempio, l’indice zero per segnalare che quel pixel non appartiene allo sprite, ma dovrà essere visualizzata la grafica dello schermo. In questo modo si potrebbe fare completamente a meno della maschera e quindi questa primitiva diventerebbe identica a quella di spostamento di regioni rettangolari (incluso il numero di accessi necessari alla memoria).
Con uno schermo a 8 colori significherebbe sacrificarne uno per la maschera, e utilizzare i rimanenti 7 per lo “sprite” vero e proprio. Potrebbe sembrare un grosso sacrificio, ma bisogna considerare che tale scelta è stata molto comune anche nei giochi su piattaforme aventi grafica planare, che dunque hanno in ogni caso “perso” (non utilizzato) un colore, pur avendo avuto la possibilità di fruttarlo. Questo perché, dovendo realizzare oggetti a 8 colori, i grafici dell’epoca utilizzavano i programmi di grafica sempre con schermi a 8 colori (anziché 16; per risparmiare spazio su disco), per cui si vedevano poi costretti a non usare il primo per riservarlo ai “buchi”. In ogni caso l’impatto risulta mitigato e addirittura trascurabile all’aumentare del numero dei colori.
Per contro c’è da dire che la grafica planare presenta anche dei vantaggi rispetto a quella packed, quando bisogna operare su meno bitplane rispetto alla profondità di colore.
Un esempio classico, che peraltro abbiamo implementato in Fightin’ Spirit (gioco per l’Amiga), è quello della visualizzazione dell’ombra dei personaggi in un videogioco. In questo caso l’ombra (raffigurata come un ellisse ai piedi del giocatore) è costituita da un solo bitplane, per cui disegnarla sullo schermo richiede la modifica di un solo bitplane (perché il gioco utilizzava la cosiddetta modalità Half-Brite dell’Amiga, dove un bitplane segnalava al controllore grafico se utilizzare il colore a luminosità dimezzata oppure piena di uno dei 32 colori selezionati e codificati nei rimanenti 5 bitplane).
In questo caso la grafica planare risulta di gran lunga più efficiente, perché l’equivalente operazione su un sistema packed avrebbe pesato 6 volte (visto che il gioco era a 64 colori = 6 bitplane), in quanto cambiare un solo bit in tutti i pixel “toccati” dall’ombra comporterebbe necessariamente la lettura, modifica, e scrittura di tutti i byte che in essa ricadrebbero.
Ciò non toglie che si tratti, comunque, di casi particolari e poco comuni. Infatti quel gioco (come tutti) è dominato pesantemente da operazioni di copia di regioni rettangolari (per ripristinare il fondale dello schermo, dopo che sono stati disegnati i personaggi) e, soprattutto, da operazioni di inserimento con mascheramento (per disegnare i personaggi, “incastrandoli” sul fondale). Tenendo conto di tutto, il guadagno relativo al tracciamento delle ombre rimane ben poca cosa.
Questo chiude le analisi e valutazioni dei pregi e difetti dei formati grafici planare e packed, e dimostra come quasi sempre il secondo risulti più efficiente in termini di banda di memoria utilizzata nonché di spazio (di questo magari ne parlerò meglio e più in dettaglio in un articolo appositamente dedicato all’Amiga).
In sintesi, la grafica planare paga proprio in termini di suddivisione degli indici colore in bitplane che risiedono in differenti zone di memoria, oltre che alla dimensione del bus dati (e al relativo allineamento di cui tenere conto): più aumentano i bitplane e/o più aumenta la dimensione del bus dati (e relativo allineamento), e più inefficiente diventa. La grafica packed risulta, invece, ben più efficiente con l’aumentare della dimensione del bus dati; mentre l’aumento del numero di colori fa perdere via via in efficienza, ma in maniera più ridotta.
Col termine efficienza mi sono limitato alla banda di memoria e/o allo spazio occupato, perché sono quelle che sostanzialmente dettano i limiti del sistema quando i programmatori devono implementare qualcosa. Ho preferito non tenere conto, in questo contesto, della complessità circuitale relativa all’implementazione del controllore grafico o di coprocessori come il Blitter e, più in generale, di come si potrebbero realizzare in hardware le primitive grafiche, sempre per evitare di far esplodere le dimensioni del pezzo, ma la situazione sarebbe simile (ma maggior parte sarebbe più semplice ed efficiente da implementare con la grafica packed).
Ribadisco, infine, che l’analisi è stata basata su grafica a 8 colori = 3 bit, ma esclusivamente per semplificare e non appesantire la trattazione. Tale scelta non limita i risultati ottenuti esclusivamente a questo caso, perché informazioni simili si possono ottenere considerando grafica a 16, 32, 64, 128, 256 colori, ed è sufficiente ripercorrere fedelmente tutti gli esempi di cui sopra per ottenere i dati relativi alla specifica profondità di colore analizzata.
All’aumentare del numero di colori si verificano più casi in cui la grafica packed presenta sovrapposizioni (è necessario accedere a due byte anziché a uno solo per leggere e/o modificare l’indice del colore di un pixel), ma complessivamente rimane quasi sempre più efficiente rispetto a quella planare. Infatti non bisogna dimenticare che gli scenari in cui la grafica planare risulti più efficiente di quella packed si verifichino esclusivamente per il caso migliore della prima e quello peggiore per la seconda; i casi migliori della grafica packed sono sempre ben distanti (nettamente a suo favore, ovviamente) da quelli migliori per quella planare, e lo stesso si verifica per quelli peggiori (dove quella planare spesso fa registrare numeri di gran lunga superiori).
Mi scuso per l’eccessiva lunghezza, ma ritengo che una trattazione dettagliata e con parecchi (freddi) numeri alla mano fosse necessaria per confutare in maniera solida e ben argomentata una così radicata leggenda metropolitana, senza che fosse lasciato ancora spazio a dubbi e insinuazioni.