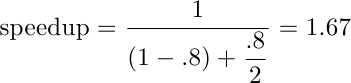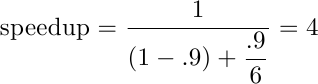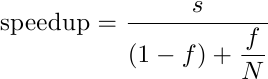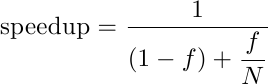
Il pipelining è una tecnica relativamente semplice ed estremamente efficace per aumentare le prestazioni dei processori: qualitativamente, spezzando la logica su più stadi è possibile avere più istruzioni in-flight nello stesso momento, aumentando il throughput. È però possibile analizzare in modo quantitativo questo aumento di performance. Per farlo, si può usare una delle regole base più usate nell’ambito dell’architettura dei calcolatori: la legge di Amdahl.
La legge di Amdahl
Questa “legge” prende il nome da Gene Amdahl, famoso Computer Architect uscito dalle fucine di talenti della IBM degli anni ’50/’60. La legge è estremamente semplice e permette di calcolare l’incremento delle prestazioni di un sistema dato l’aumento di prestazione di un suo sottocomponente:
dove f è la frazione del sistema che viene accelerata e N è l’accelerazione. Come si vede, è una sorta di media armonica tra la frazione accelerata e quella non accelerata.
Esempio: si consideri un programma di calcolo numerico, dominato da istruzioni floating-point, e si supponga che del tempo di esecuzione di 10 minuti, 8 sono di floating-point e 2 di altro. Se costruiamo un nuovo processore capace di prestazioni fp doppie, il programma ci metterà in totale 6 minuti: 4 per le floating-point, dimezzate, e 2 per il resto, invariate. L’aumento di prestazioni complessivo sarà 10/6 = 1.67, cioè il 67%. Volendo usare la legge di Amdahl, la frazione accelerata è l’80% (8 minuti su 10), e l’accelerazione è 2, quindi
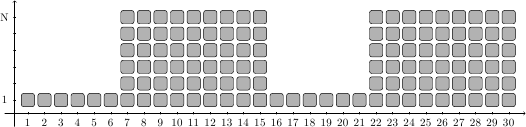
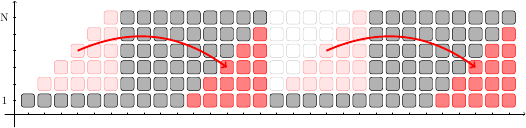
Questa regola si applica bene anche al caso di processori vettoriali, dove si alternano porzioni di codice sequenziale (una sola istruzione eseguita per ciclo di clock) a porzioni di codice vettoriale (N istruzioni per ciclo di clock). Un esempio è mostrato in figura:
dove sull’asse X si susseguono i colpi di clock e sull’asse Y troviamo il numero di istruzioni in esecuzione in un dato istante. Ogni quadratino è un’istruzione in-flight nel processore.
In questo esempio ideale si alternano 6 istruzioni sequenziali, che prendono 6 cicli di clock, a 54 istruzioni vettorizzabili, che eseguono in soli 9 cicli di clock, 6 alla volta. La legge di Amdahl ci permette di calcolare l’aumento di prestazioni rispetto ad un processore scalare (capace di una sola istruzione per ciclo di clock). La frazione accelerata è 54/(54+6)=.9, cioè il 90%, mentre l’accelerazione è di 6 (pari all’ampiezza del vettore):
Il programma viene accelerato di 4 volte. Possiamo facilmente controllare la correttezza del risultato: il processore scalare impiegherebbe 60 cicli di clock ad eseguire le istruzioni, mentre il processore vettoriale ci mette 6 cicli per la parte sequenziale e 9 per la parte vettoriale, cioè 15 cicli in tutto: è effettivamente 4 volte più veloce.
Legge di Amdahl applicata alla pipeline
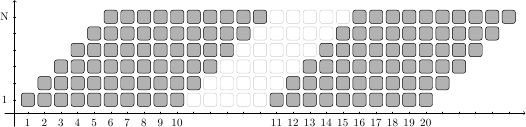
Applicare la legge di Amdahl ai processori vettoriali è semplice e intuitivo. Più interessante è notare che lo stesso identico ragionamento può essere applicato ai processori scalari ma pipelinizzati. Usando la stessa rappresentazione precedente, è possibile raffigurare le istruzioni in-flight nel processore in questo modo:
Sull’asse X ora ci sono le istruzioni lanciate in pipeline (i numeri si riferiscono alle istruzioni, mentre ogni tick è un ciclo di clock), mentre sull’asse Y ci sono gli stadi della pipeline. Le istruzioni si “muovono” in diagonale, andando verso destra e verso l’alto. Ad esempio, la prima istruzione è nello stadio 1 al ciclo 1, e raggiunge l’ultimo stadio al ciclo 6.
Nell’esempio in figura, 10 istruzioni vengono lanciate in pipeline in successione e poi si verifica uno stallo di 5 cicli: solo quando l’istruzione 10 esce dalla pipeline l’istruzione 11 può entrare nel primo stadio. In totale sono stati riempiti 60 “slot” (6 stadi per istruzione per 10 istruzioni) su 15 cicli di clock (tra quando l’istruzione 1 entra in pipeline a quando l’istruzione 10 esce dalla pipeline): un aumento delle prestazioni di un fattore 4, lo stesso risultato del caso precedente!
Non è un caso: per capire come mai, è possibile “riorganizzare” le istruzioni nei vari stadi, “spostandole” tra diversi slot per costruire la seguente immagine:
Ritagliando istruzioni da una parte e incollandole dall’altra si ottiene esattamente lo stesso schema di riempimento che avevamo per il processore vettoriale: 6 cicli con solo uno slot occupato, seguiti da 9 cicli con tutti e 6 gli slot occupati. Naturalmente, “tagliare” e “incollare” istruzioni da uno slot all’altro non ha alcun significato fisico, è solo un modo pittorico di dimostrare l’equivalenza.
Questo dimostra in modo più formale da dove viene l’aumento di prestazioni in una pipeline: il parallelismo temporale di una pipeline è equivalente al parallelismo spaziale di un processore vettoriale, e la legge di Amdahl ci permette di calcolare l’aumento di prestazioni in entrambi i casi. Nel caso della pipeline, N è il numero di stadi (e non l’ampiezza del vettore) e f dipende dalla frazione di codice non affetto da bolle (cioè stalli) nella pipeline.
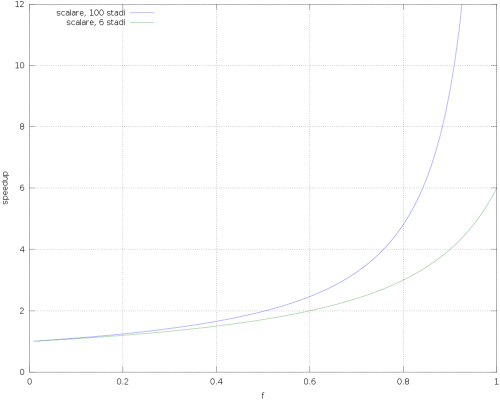
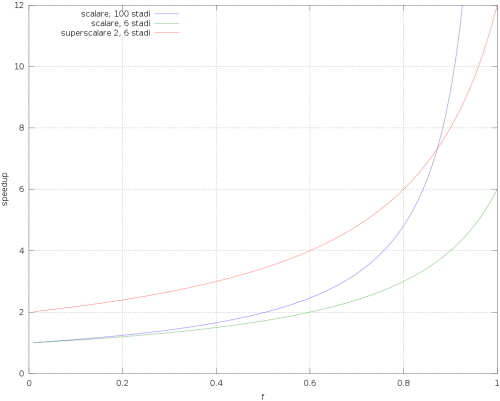
Ciò detto, è molto interessante tracciare un grafico che mostra l’aumento complessivo delle prestazioni a seconda della frazione di codice accelerato f:
In figura vediamo due diversi scenari: in verde, un processore scalare con 6 stadi di pipeline; in blu, un processore sempre scalare ma con 100 stadi. La cosa più importante da notare è che le prestazioni scendono molto velocemente appena f scende sotto l’unità (cioè non tutto il codice è accelerabile), e scendono tanto più drammaticamente quanto più la pipeline è profonda (o il vettore è largo: abbiamo visto che il modello è lo stesso). Per una frazione di codice parallelizzabile del 90% (molto alta) l’ipotetico processore con 6 stadi ha uno speedup di 4 (cioè il 33% meno del massimo), ma il processore con 100 stadi ha uno speedup di solo 9, cioè il 91% meno del massimo!
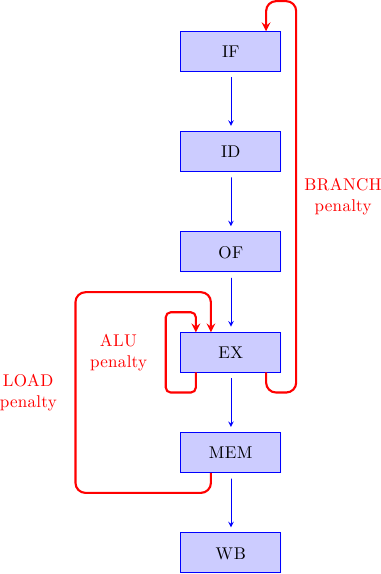
Questo mostra un concetto fondamentale: man mano che le pipeline diventano più profonde (cioè con più stadi) gli stalli hanno un impatto sempre maggiore sulle performance. Nell’esempio precedente, con f = 90% l’ipotetico processore con 100 stadi sarebbe poco più del doppio più veloce di quello con 6 stadi (e meno per f più basse), ma in confronto sarebbe molto più difficile da costruire e avrebbe consumi assolutamente insostenibili (visto che il consumo energetico aumenta circa col cubo della frequenza). La realtà sarebbe anche peggio: gli stalli vengono dalle dipendenze dati e controlli, descritte qui e sintetizzate in figura
All’aumentare della profondità della pipeline il numero di stalli cresce (perchè gli anelli di dipendenza diventano più lunghi), f diminuisce, e le prestazioni crollano (rispetto al massimo teorico) ancora più rapidamente.
La legge di Amdahl, quindi, oltre a permetterci di calcolare le performance, ci fa capire come pipeline estremamente profonde siano altamente problematiche per la maggior parte del codice: non è possibile aumentare le performance a piacimento semplicemente aumentando gli stadi, ma è necessario pensare a qualcosa di completamente diverso.
Oltre la pipeline singola: i processori superscalari
Partendo dall’idea più semplice, possiamo pensare di costruire un processore superscalare “incollando” s pipeline semplici una di fianco all’altra. Ad ogni ciclo di clock ci saranno quindi s istruzioni di cui viene fatto il fetch, s istruzioni in decodifica, s istruzioni in esecuzione, e così via. Da notare che questo è diverso da un processore vettoriale, dove una sola istruzione porta all’esecuzione di s operazioni.
Supponiamo per un momento che sia effettivamente possibile trovare ed eseguire s istruzioni indipendenti per ciclo di clock. Il grafico precedente, che mostrava le istruzioni in-flight nella pipeline, verrebbe modificato nel seguente modo: ogni “slot” si moltiplicherebbe in s slots, corrispondenti alle s istruzioni parallele. L’aumento di performance di questo modello supersemplificato sarebbe, ovviamente, s; la legge di Amdahl si modificherebbe in questo modo:
dove s è la superscalarità, N è sempre il numero di stadi di pipeline e f è sempre la frazione di codice accelerabile dalla pipeline. Qual è l’impatto di s sulle performance? Aggiungiamo al grafico precedente il nuovo modello (in rosso), con due pipeline parallele profonde 6 stadi:
Il risultato è stupefacente: le prestazioni del nuovo processore, oltre ad essere ovviamente il doppio della pipeline singola con lo stesso numero di stadi, sono molto migliori anche della pipeline singola a 100 stadi! Nel range tipico della maggior parte delle applicazioni (f tra 40% e 80%) l’ipotetico processore superscalare è sempre più veloce della pipeline profondissima, con prestazioni in alcuni casi quasi doppie nonostante la pipeline sia 16 volte più corta! Il “miracolo” è dato dal fatto che una pipeline corta e larga soffre meno a causa degli stalli (perchè corta) e produce più lavoro per ciclo di clock (perchè larga). Usando meno parallelismo temporale e più parallelismo spaziale otteniamo un risultato molto migliore.
In questa analisi supersemplificata abbiamo assunto che sia sempre possibile mandare s istruzioni nelle pipeline laddove la pipeline semplice ne manda una. Questa è un’assunzione estremamente ottimistica: la domanda che ci dobbiamo porre ora è se esiste davvero abbastanza ILP (Instruction-Level Parallelism), cioè istruzioni che possono essere eseguite parallelamente, e come sfruttarlo in un’architettura reale.
Dov’è l’Instruction Level Parallelism?
In un programma “normale” quante istruzioni possono essere eseguite contemporaneamente? Cosa limita questo parallelismo? Quale architettura è possibile realizzare in modo pratico per estrarre questo ILP? Queste domande sono state di fondamentale importanza per i Computer Architect dagli anni ’70 fino ai ’90 (e sono importanti ancora oggi, anche se il parallelismo tra core e tra thread è ora più importante del parallelismo tra istruzioni nello stesso thread, che è già stato sfruttato quasi allo stremo).
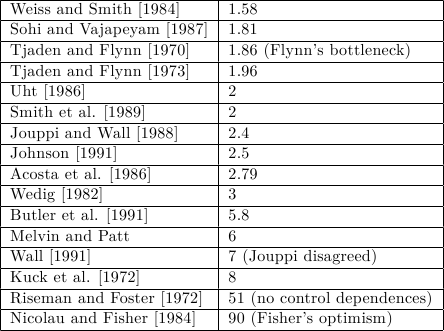
Un gran numero di paper sono stati scritti sul limite massimo di ILP sfruttabile nei programmi. Alcuni dei risultati classici sono presentati in tabella:
Salta subito all’occhio come i diversi numeri differiscano in modo estremo. Due dei più famosi (abbastanza da meritarsi un soprannome loro) sono il “collo di bottiglia di Flynn”, decisamente pessimista sul massimo ILP sfruttabile, e lo “ottimismo di Fisher”, che al contrario mostra un’enorme quantità di ILP utilizzabile.
Per capire l’origine di queste differenze, bisogna considerare che i diversi studi assumono diverse condizioni al contorno: tecniche per i compilatori, riordinamento dei blocchi base (che sono sequenze di istruzioni non interrotte da salti, e in cui non si può saltare), speculazione sulle dipendenze di controllo e altre tecniche più aggressive possono trasformare il codice per esporre più ILP senza modificare il significato del programma.
Si consideri ad esempio questo pezzo di codice:
r1 <= r2 + 1 r3 <= r1 / 17 r4 <= r0 - r3
Ogni istruzione dipende dalla precedente: le istruzioni vanno eseguite serialmente, e l’ILP è pari a 1 (3 istruzioni in 3 cicli di clock). Consideriamo quest’altro codice:
r11 <= r12 + 1 r13 <= r19 / 17 r14 <= r0 - r20
Sono le stesse operazioni, ma qui non esiste alcuna dipendenza tra esse: ora ILP = 3 (3 istruzioni in 1 ciclo di clock). Ma se combiniamo insieme i due blocchi:
r1 <= r2 + 1 r3 <= r1 / 17 r4 <= r0 - r3 r11 <= r12 + 1 r13 <= r19 / 17 r14 <= r0 - r20
otteniamo un unico blocco con ILP = 2 (6 istruzioni in 3 cicli di clock). La morale è che lo scope ha importanza: più un blocco base è grosso, più è facile trovare istruzioni indipendenti che possono essere eseguite in parallelo. Da qui tecniche come il loop unrolling, speculazione dei salti, fusione di blocchi base con codice di recupero ed altre tecniche che espongono più ILP aumentando la dimensione dei blocchi base.
Per riassumere, il “collo di bottiglia di Flynn” è veramente troppo pessimistico, ed esiste abbastanza ILP da permetterci di costruire processori superscalari.
Conclusione
In questo articolo abbiamo visto che esiste abbastanza ILP (e che esistono tecniche per incrementarlo) da costruire processori superscalari, e che lo sfruttamento di questo ILP aumenta di molto le prestazioni della CPU.
Nei prossimi articoli vedremo diverse tecniche per costruire fisicamente processori in grado di eseguire più istruzioni per ciclo di clock.