Nella scorsa puntata avevamo iniziato a gettare uno sguardo sulle componenti di rumore tipiche di un processo di acquisizione ed elaborazione delle immagini digitali.
Per chiarire bene determinati concetti, era stato necessario introdurre lo schema a blocchi di un sensore digitale (avevamo preso, in particolare, come esempio, un cmos) e di alcuni suoi elementi, visti un po’ più in dettaglio. Avevamo visto come alcune ocmponenti di rumore, quelle con pattern di tipo “fisso”, siano più facilmente filtrabili mentre altre che hanno la “sinistra caratteristica” di variare nel tempo, a causa della loro imprevedibilità possono solo essere trattate in modo da ridurre il loro impatto negativo sulla qualità d’immagine.
Dalle considerazioni fatte nella parte finale, ma anche da quelle fatte sull’efficienza quantica, è emerso che anche in fotografia le “dimensioni contano” e nello specifico, è meglio avere sensori di dimensioni maggiori, a parità di numero di pixel, sia per ridurre gli effetti della diffrazione, sia per limitare quelli delle interferenze di tipo elettrico, ma anche per avere un miglior rapporto segnale/rumore di tipo quantico. Anche se in questo contesto stiamo limitando l’attenzione alla gestione del rumore, sensori di dimensioni maggiori permettono anche una miglior gestione della profondità di campo, come sta illustrando Matteo nei suoi ottimi articoli.
Ovviamente, queste considerazioni non devono necessariamente portare alla conclusione che si debbano acquistare solo full frame con ottiche professionali e neppure ha lo scopo di stigmatizzare la corsa ai Mpixel. Sensori di piccole dimensioni, sempre più affollati propongono sfide senpre più ardue, ma anche stimolanti, da vincere, sulla gestione del rumore e sulla risolvenza dei sistemi lente-sensore, che portano a ricercare continuamente nuovi materiali e tecnologie per migliorare la qualità d’immagine.
E’ altrettanto ovvio, però, che la qualità di uno scatto non è misurabile col numero di pixel e che i 10 Mpixel di una G11, ottima macchina ma pur sempre “compatta”, non valgomo i 10 Mpixel di una EOS 400D, di una Nikon D60 o di una Olympus E520 (tanto per citare tre fotocamere reflex entry level aventi sensori con differenti tecnologie) sia a livello di gestione della PdC che del rumore o degli effetti della diffrazione.
Fatto questo preambolo, torniamo a quello che è l’argomento principale di questa trattazione, ovvero il rumore digitale, la sua origine e la sua gestione.
Due settimane fa avevamo visto come l’insieme dei parametri di un dispositivo di acquisizione ed elaborazione delle immagini sia schematizzabile con il, cosiddetto, Camera Response Function ovvero con la funzione f(CR) che riassume le caratteristiche del sistema lente-sensore-elettronica.
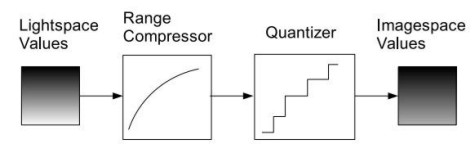
Questa funzione è, a sua volta, scomponibile in due ulteriori funzioni non lineari, la prima delle quali indicata, nella figura sottostante, come range compressor, riassume tutte le caraterristiche di ciò che è a monte del circuito di quantizzazione mentre la seconda, indicata come quantizer, riunisce proprio le caratteristiche di quest’ultimo elemento.
Se, dunque, il primo blocco comprende parametri come l’efficienza quantica e la risposta in frequenza del sistema e tiene conto dekke componenti del rumore viste negli scorsi capitoli, il secondo blocco è quello che fornisce informazioni sulla qualità della codifica digitale del segnale.
Nel trattare l’antialiasing avevo fatto cenno ai meccanismi di campionamento e quantizzazione, per cui non mi dilungherò sulla cosa.
Inoltre, credo sia superfluo sottolineare il fatto che l’utilizzo di un maggior numero di bit implichi una maggior precisione di calcolo che, nel caso specifico, si traduce in una maggior gamma dinamica e una più fedele rappresentazione dei colori a parità di qualità degli algoritmi utilizzati. Questo spiega il motivo per cui i 12 o i 14 bit per canale di uno scatto in RAW forniscano una miglior base di partenza, per chi si diletta di fotoritocco, rispetto agli 8 bit di un jpg.
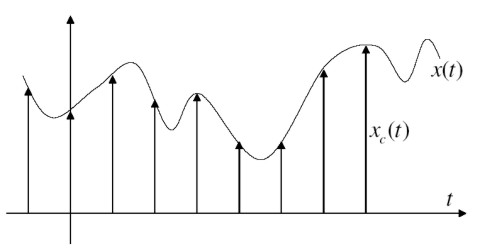
Le operazioni di campionamento e di quantizzazione, però, introducono a loro volta degli errori. Partiamo dalla prima:
se sono rispettate le condizioni del teorema di Shannon, l’operazione di campionamento non fa perdere informazioni sul segnale originario. Ci sono situazioni, però, in cui non è possibile rispettare le condizioni imposte dal teorema di Shannon e, in tal caso si hanno disturbi noti, genericamente, con il nome di aliasing.
Quella che sicuramente introduce errori, indipendendentemente dal tipo di algoritmo utilizzato, è l’operazione di quantizzazione. Per i non addetti ai lavori o per chi non ha dimestichezza con la teoria dei segnali, una volta che si è deciso quanti e quali campioni di un determinato segnale sono da considerarsi significativi, si passa al vero e proprio processo di trasformazione del segnale in sequenza numerica; ovvero, si decide, per ciscun campione, quale quantità di informazioni sia necessaria.
Questo si traduce, nella pratica, in una scelta sul numero di bit per ciascun campione preso e, nel caso di un fotosito, di conseguenza, sul numero di bit per ciascuno dei 3 colori base adoperati. Più bit significano più livelli, ossia più gradazioni di colore o, se si preferisce, un maggior numero di sfumature per ogni colore. Abbiamo visto, però, che i singoli fotodiodi sono monocromatici e che è il filtro (nel caso do matrice bayer) o la disposizione stratigrafica (nel caso di tecnologie X3) a fornire informazioni sulle relative componenti cromatiche. Quindi, di fatto, per ciascun fotosito sarebbe corretto parlare di livelli di grigio e non di livelli “colore”. Per intenderci, se, ad esempio, questo è il risultato finale
l’immagine catturata dal sensore, scomposta nelle tre componenti cromatiche è questa
ed è solo in fase di ricostruzione che, o grazie alle informazioni fornite dalla maschera a matrice bayer o a quella derivanti dalla stratigrafia dei layer (foveon) che le tre componenti vengono “interpretate” nel modo seguente
ossia viene “aggiunto” il colore.
Il motivo per cui questo processo introduce errori è facilmente intuibile: si tenta di rappresentare un’immagine continua con infinite sfumature di colore (anche se l’occhio è in grado di percepire solo una parte della radiazione che, riflessa dall’oggetto visualizzato, colpisce il bulbo oculare) in forma discreta e con un numero finito di livelli di colore. Inoltre, l’immagine è catturata come “livelli di grigio” reinterpretata come composizione di 3 immagini una per ciascuna componente cromatica e ricostruita mediante interpolazione. Ciascuno di questi passaggi introduce una o più fonti di rumore alcune delle quali già viste e qualcun altra che andremo ad esaminare.
La scelta più semplice da effettuare è quella che si basa sul puro e semplice valore dell’intensità del segnale, ovvero sul numero di fotoni che colpiscono ogni fotosito in un determinato intervallo di tempo. Il problema di questo tipo di algoritmi è che la loro risposta è lineare in frequenza mentre quella dell’occhio umano è di tipo logaritmico. Messa così la cosa, appare evidente che, non potendo avere la velleità di riprodurre fedelmente l’immagine, l’unica strada percorribile sia quella di cercare di avvicinarsi il più possibile a quella che è la risposta dell’occhio umano che dell’immagine prodotta è l’utilizzatore finale.
Di conseguenza, si cerca di implementare algoritmi di quantizzazione che forniscano risposte di tipo logaritmico, in modo da espandere le basse luci e comprimere le alte. I passi da fare sono, dunque: compressione, quantizzazione e decompressione. Questo procedimento permette di “recuperare” le parti scure dell’immagine come illustrato in basso dove, la stessa immagine in B/N è quantizzata liearmente sulla sinistra e logaritmicamente sulla destra
Parlando di quantizzazione abbiamo parlato di errore e non di rumore; in effetti, però, a condizione che:
- l’intervallo di quantizzazione sia di piccola ampiezza
- il numero di bit utilizzato sia “elevato”
- il segnale analogico digitalizzato occupi una banda continua in frequenza
- il segnale analogico abbia distribuzione di ampiezza uniforme entro ciascun intervallo di quantizzazione,
per poter assimilare l’errore di quantizzazione ad un rumore bianco.
L’utilizzo di un numero elevato di bit per livello, però, ha delle controindicazioni: innanzitutto a livello di occupazione di spazio in memoria e, in secondo luogo, nella generazione di errori. La prima affermazione appare ovvia, in quanto un maggior numero di informazioni necessità di un più ampio spazio in memoria. In quanto alla seconda
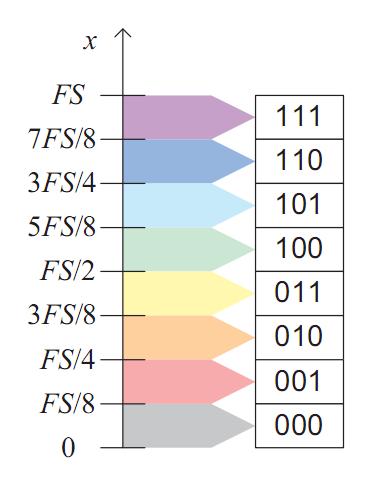
In questo esempio di quantizzazione di tipo uniforme, che fa uso di soli 3 bit, ad ogni sample sono dedicati 8 intervalli, ognuno dei quali corrispondenti ad uno degli 8 valori ottenibili con gli 8 bit. Ognuno di questi 8 intervalli ha un valore di soglia (posto al centro dell’intervallo) che viene adoperato per confrontare il valore del segnale in quel determinato punto (o fotosito) con quello che dovrebbe corrispondere a quel preciso valore numerico. Quanto più il valore del segnale si discosta dalla soglia tanto più è elevata la possibilità di errore nell’interpretazione del corretto valore. Avere più bit per ogni canale (o per ogni fotosito) equivale ad avere lo stesso intervallo (in figura compreso tra 0 e FS) suddiviso in un maggior numero di intervalli di dimensioni inferiori rispetto a quelli dell’immagine. Chiaro, a questo punto, che una codifica con due soli livelli presenta, sotto questo profilo, probabilità d’errore di molto inferiore mentre avere tanti bit può far aumentare la probabilità di una non corretta interpretazione di qualche valore. Ovviamente non è possibile pensare ad una fotografia codificata ad 1 solo bit e si deve cercare un compromesso tra numero di livelli di colore che si vuole rappresentare e complessità dell’algoritmo e dei circuiti impiegati per la codifica stessa e per la predizione e la correzione di eventuali errori. Questo è uno dei motivi per cui fotocamere di livello più alto, che fanno uso di 14 o, addirittura, di 16 bit per canale, hanno costi più elevati di fotocamere che impiegano solo 8 o, al massimo, 12 bit per canale.
A complicare le cose, interviene il rumore, in tutte le forme viste sin qui, che fa traslare i livelli del segnale “letto” rispetto a quelli effettivi e li fa discostare dai valori delle soglie, dando luogo a errori nella rappresentazione dei colori anche a livello di singolo fotosito o pixel. Anche in questo caso, fotocamere di fascia più alta implementano algoritmi più complessi e sofisticati che permettono di limitare gli errori di “interpretazione” o di distribuirli più uniformemente in frequenza (questo aspetto lo affronteremo in futuro).
A questo punto, sorge spontanea la domanda: ma se la digitalizzazione delle immagini comporta tutti questi problemi e presenta tutti questi limiti, allora perchè la utilizziamo? La risposta è semplice: perchè anche gli altri strumenti che abbiamo a disposizione per catturare immagini e visualizzarle sono, a loro volta, limitati. Lo è l’occhiuo umano, lo è la pellicola che può arrivare la massimo a 11 eV; lo sono i migliori monitor che non superano i 10 eV.
A questo punto appare chiaro che i limiti della digitalizzazione diventano accettabili di fronte alla possibilità di manipolare le immagini a proprio piacimento più questa possibilità viene enfatizzata, più i vantaggi del digitale diventano evidenti. Per questo motivo, ad esempio, si sta investendo così tanto sulla tecnologia MOS che rispetto ai CCD, in origine, presentava pesanti limitazioni in fatto di corrente di soglia e di efficienza quantica (e quindi di gamma dinamica) oltre che di uniformità di risposta alla luce incidente.
A fronte di questi svantaggi iniziali (ormai praticamente colmati) la tecnologia MOS permette una gestione dell’immagine accurata e puntuale (addirittura per pixel o singolo fotosito) a possibilità di manipolazione pressochè illimitata.