Prosegue in questo post la serie di post che presentano come soggetto l’energia solare.
Nello scorso post è stata introdotto l’argomento generale, e si è parlato della radiazione extraterrestre, mentre in questo post verrà affrontato il tema della radiazione che attraversa l’atmosfera, e la valutazione dell’irraggiamento su una superficie arbitrariamente orientata collocata sul suolo terrestre.
RADIAZIONE TERRESTRE
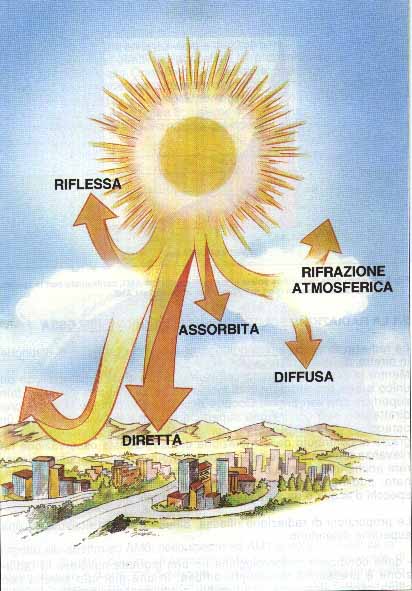
La radiazione solare incidente sulla Terra subisce l’influenza dell’atmosfera, in particolare una quota di tale radiazione viene nuovamente riflessa nello spazio, una quota viene assorbita dall’atmosfera stessa ed una quota viene diffusa dall’atmosfera secondo il fenomeno dello scattering:
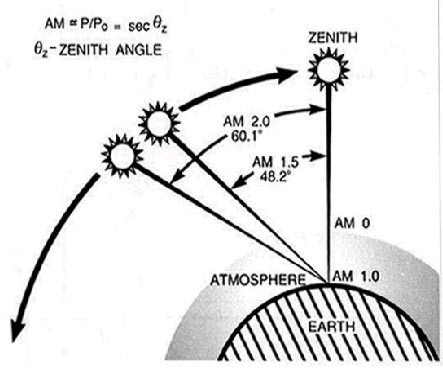
Il processo di assorbimento della radiazione da parte dell’atmosfera è funzione dell’angolo effettivo α (introdotto nel precedente post), il quale influenza lo spessore di atmosfera attraversato dai raggi solari (indicato con AM in figura), per tenere conto di ciò è stata definita la massa d’aria unitaria AM1 (Air Mass One) come lo spessore di atmosfera standard misurato al livello del mare attraversato perpendicolarmente alla superficie dai raggi del Sole, mentre con AM0 si indica la condizione extratmosferica:
Misurando la radiazione solare a livello del mare, a mezzogiorno ed in condizioni atmosferiche ottimali si misurerà sempre un valore di radiazione inferiore alla costante solare (Cs = 1367W/m2 circa), in particolare per tali condizioni ottimali si può ottenere un valore dell’ordine dei 1000W/m2, ma risulta evidente come questo valore vari sensibilmente al variare delle condizioni atmosferiche.
RADIAZIONE DIRETTA, DIFFUSA E RIFLESSA
La radiazione solare terrestre si può suddividere in tre componenti, ognuna delle quali fornisce un contributo alla radiazione misurabile in un dato sito, in particolare si parla di radiazione diretta, diffusa e riflessa.
La radiazione diretta incide su una superficie con un ben definito ed unico angolo di incidenza, la radiazione diffusa invece non presenta un solo angolo di incidenza ma incide sulla superficie da molteplici direzioni, mentre la radiazione riflessa deriva dalla riflessione dovuta all’ambiente circostante.
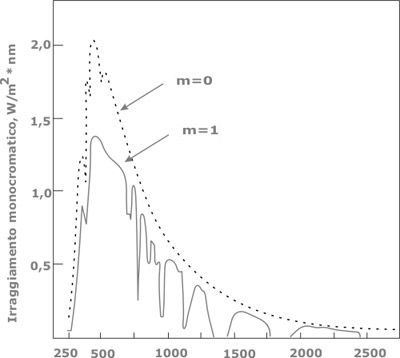
Nella seguente figura si può vedere rappresentato l’irraggiamento monocromatico al suolo (m = 1) ed all’esterno dell’atmosfera (m = 0)
Esaminando l’irraggiamento diretto al suolo e l’irraggiamento extratmosferico incidenti sulla normale alla superficie (ovvero perpendicolarmente), è possibile determinare il coefficiente di trasmissione della radiazione diretta τb, che in condizioni di sereno vale:
τb = 0.5exp[-0.65m(z,α)]+ 0.5exp[-0.095m(z,α)]
Con m(z,α) si indica la massa d’aria ad una determinata quota z ed angolo di altezza solare α e si valuta in funzione di un valore di riferimento sul livello del mare secondo la relazione:
m(z,α) = m(0,α)p(z)/p(0)
dove p(z) rappresenta la pressione atmosferica alla quota z e p(0) la pressione atmosferica sul livello del mare.
La massa d’aria sul livello del mare si può valutare secondo la seguente relazione:
m(0,α) = [1229 + (614sen α)2]0.5 – 614sen α
E’ ora immediato ricavare le quote di irraggiamento diretto incidente perpendicolarmente alla superficie e diffuso al suolo sul piano orizzontale, sempre per condizioni atmosferiche di sereno:
Ibn = I0τb
L’irraggiamento diffuso al suolo si valuta utilizzando la correlazione di Liu-Jordan:
τd = 0.2710 – 0.2939τb
Ido = (Io sen α) τd
Tali equazioni sono di difficile applicazione in quanto la notevole imprevedibilità delle condizioni atmosferiche rendono difficile il loro utilizzo, ma restano comunque valide dal punto di vista didattico.
RADIAZIONE SU UNA SUPERFICIE INCLINATA
Un qualunque impianto, sia esso solare termico, fotovoltaico o termodinamico, sarà orientato in modo da ricevere quanta più radiazione possibile nei sui pannelli captatori, pertanto è importante individuare le grandezze corrispondenti.
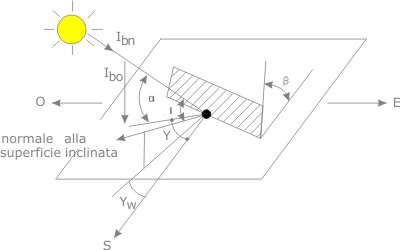
L’inclinazione della superficie rispetto al piano orizzontale è indicata con l’angolo β e si chiama angolo di tilt, mentre l’orientamento rispetto alla direzione Sud è rappresentata dall’angolo γ che rappresenta l’angolo di azimut.
Il valore β = 0° indica la superficie completamente orizzontale, mentre γ = 0° indica la direzione della superficie perfettamente a Sud (tipicamente γ è positivo per rotazioni verso ovest e negativo per rotazioni verso est).
Per valutare ora la radiazione diretta incidente su un pannello arbitrariamente orientato si consideri tale radiazione incidere secondo un arbitrario angolo υ rispetto alla superficie del pannello (posizionata a β e γ stabiliti).
In un dato istante (ed in funzione della località alla latitudine φ) si avrà a disposizione il valore degli angoli δ e ω (introdotti nel precedente post), e si potrà valutare la radiazione diretta incidente mediante la relazione:
Gb = IboRb
Dove Rb rappresenta il fattore di inclinazione della radiazione diretta:
Rb = cos υ /sen α
Per chi non resiste alla curiosità, la relazione che definisce cos υ risulta parecchio complessa e la riporto per completezza:
cos υ = sen δ(sen φ cos β – cos φ sen β cos γ) + cos δ cos ω(cos φ cos β + sen φ sen β cos γ) + cos δ sen β sen γ sen ω
La radiazione diffusa incidente sulla stessa superficie inclinata è data da:
Gd = IdoRd
Dove Ido rappresenta la radiazione diretta ed Rd il fattore di inclinazione della radiazione diffusa:
Rd = (1 + cos β) / 2
Per β = 0° si ottiene il massimo per la radiazione diffusa.
Resta da analizzare la radiazione riflessa:
La radiazione riflessa viene valutata a partire dal coefficiente di albedo ρ, il quale varia in funzione del tipo di materiale e risulta tabellato per una facile consultazione, e si valuta mediante la seguente relazione:
Gr = (Ibo + Ido)Rr
Dove Rr rappresenta il fattore di inclinazione della radiazione riflessa e vale:
Rr = ρ(1 – cos β) / 2
La radiazione riflessa si annulla per β = 0° mentre è massima per β = 90°.
A questo punto si può individuare la radiazione globale incidente su una superficie inclinata come la somma delle quote di radiazione diretta, diffusa e riflessa:
G = Gb + Gd + Gr
I valori di radiazione sono disponibili attraverso la norma UNI 10349, nella quale è disponibile la serie storica per tutti i capoluoghi di provincia con la distinzione della quota diretta e diffusa sul piano orizzontale (rispettivamente Ibo e Ido), dalle quali valutare la radiazione sulla superficie inclinata considerata.
L’ENEA mette a disposizione i dati globali storici per le varie località, sempre riferiti al piano orizzontale, non distinguendo le quote diretta e diffusa, pertanto se si vuole conoscere il valore dei singoli contributi diventa necessario ricorrere agli studi di Liu – Jordan ed alle loro correlazioni.
CONCLUSIONI
Dopo avere affrontato in questi ultimi due post questa lunga parte teorica, sarà ora possibile esaminare le varie soluzioni impiantistiche per trasformare l’energia messaci a disposizione dal Sole in energia termica ed elettrica.
Vi aspetto il prossimo lunedì mattina con la consueta rubrica Energia e Futuro.