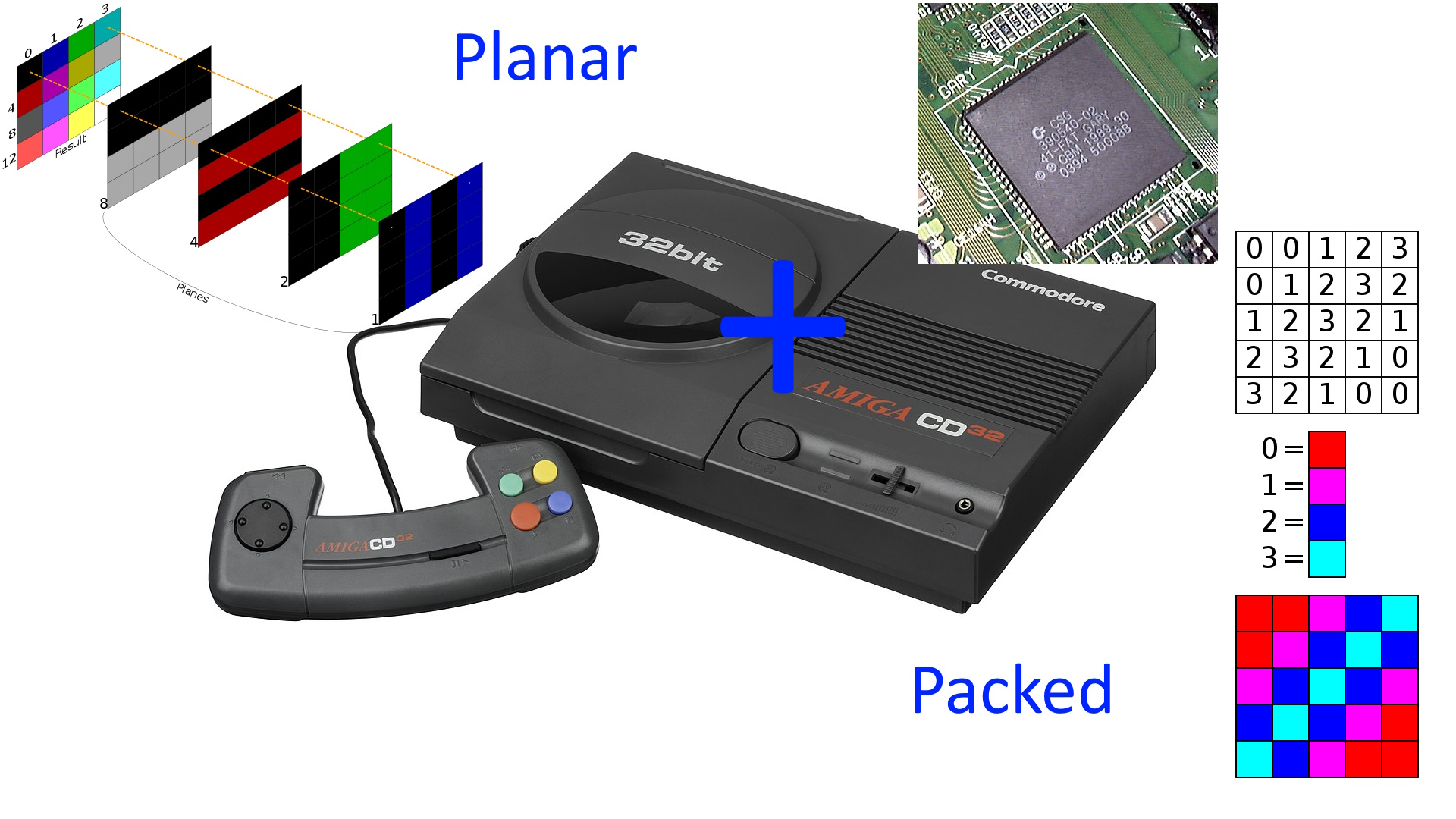
Quando si parla di grafica packed/chunky e di Amiga viene spesso tirata fuori la soluzione degli ingegneri Commodore e implementata nel chipset dell’ultima console di casa (il CD32), la quale si trova in uno dei suoi chip: Akiko.
Akiko in azione
Introdotta per cercare di prendere il treno della grafica 3D dotata di texture (fenomeno introdotto alla massa da Wolfenstein3D e successivamente consacrato da Doom, ma che aveva già mostrato il potenziale con Wing Commander), cercando di mitigare l’assenza del supporto nel chipset originale, questa trovata frutto di un pranzo fra colleghi ingegneri consta di alcuni circuiti adibiti al caricamento di 8 dati a 32 bit in formato packed a 8 bit che vengono convertiti al volo in formato planare, restituito sotto forma di altrettanti 8 dati a 32 bit da memorizzare nei rispettivi 8 bitplane. In sostanza si convertono 32 pixel a 8 bit (256 colori) da packed a planare.
I limiti di tale soluzione risultano piuttosto evidenti. La CPU deve, infatti:
- elaborare la grafica e scriverla in memoria da qualche parte;
- prelevarla 32 pixel alla volta;
- inviarla alla circuiteria di conversione chunky-to-planar;
- leggere i dati planari dalla suddetta circuiteria;
- scriverli in memoria negli appositi bitplane.
Sono tutti passaggi che consumano sia tempo della CPU sia, sopratutto, preziosa banda verso la memoria, incidendo notevolmente sulle prestazioni del gioco (come già discusso molto più in dettaglio in un precedente articolo) mentre un sistema dotato di grafica packed abbisognerebbe soltanto del primo passo se scrivesse direttamente nella memoria video o, al più, di un ulteriore passo (copiare la grafica dalla memoria di sistema a quella video) se l’accesso alla memoria video risultasse inefficiente (ad esempio con schede grafiche troppo economiche).
Non discuto ulteriormente i vantaggi dell’avere direttamente il supporto alla grafica packed, considerato che è stato oggetto di ben 17 articoli in merito che hanno sviscerato ogni singolo aspetto della questione, per cui mi concentrerò su come si sarebbe potuto aggiungere tale formato al chipset AGA col minor costo possibile (in termini sia di semplicità sia di implementazione).
Il grande ostacolo: gli slot della memoria
In effetti non è certo una questione banale, considerato che un sistema pensato per lavorare esclusivamente con grafica planare è, ovviamente, molto diverso da uno packed, come abbiamo già avuto modo di vedere in particolare negli articoli dedicati al controllore video (i primi quattro della serie), che peraltro è l’unico interessato da questo cambiamento (si può benissimo fare a meno di aggiornare anche il Blitter, lasciando che sia la CPU a gestire la grafica 3D in maniera esclusiva. Cosa che peraltro sa fare superbamente rispetto a un sistema planare).
In particolare, il problema più grosso in assoluto con l’Amiga è rappresentato non tanto dalla logica che si occupa di visualizzare la grafica, quanto da quella che legge i dati dello schermo dalla memoria grafica (Chip mem, in gergo amighista), la quale funziona coi famigerati slot di memoria, come si può approfondire in un vecchio articolo (I bitplane e le righe di raster: l’Amiga visualizza la grafica dello schermo) che tratta proprio quest’aspetto della nostra macchina del cuore.
Per cercare di riassumere e semplificare, l’Amiga (parlerò sempre del chipset AGA da qui in avanti) legge i dati di fino a 8 bitplane alla volta (anche qui, sempre per semplicità, assumerò sempre di avere 8 bitplane = 256 colori), seguendo una certa logica (illustrata nel suddetto articolo) nell’accesso alla memoria per tali dati, e una volta finita l’elaborazione (e relativa visualizzazione) passa a leggere i successi dati sempre dagli 8 bitplane, e così via finché non finisce la riga attuale, per poi ricominciare dall’inizio con quella successiva.
Si tratta di un sistema un po’ complicato che è nato da una parte per favorire al massimo gli accessi alla memoria da parte del processore Motorola 68000, e dall’altra serve per caricare i dati di ogni singolo bitplane che fa parte dello schermo. Una volta caricati tutti i dati in registri interni, il controllore video si occuperà poi di combinarli, prendendo un bit alla volta da ogni bitplane per costruire l’indice del colore, per poi accedere alla tavolozza dei colori, e finalmente prelevare il colore vero e proprio da spedire al monitor o TV.
Come già detto, il tutto è stato spiegato con dovizia di particolari nei precedenti pezzi, ma ciò che è importante ai fini di quest’articolo è mettere in chiaro che la grafica risulta distribuita negli 8 bitplane e che viene letta sfruttando gli 8 slot (accessi) di memoria a disposizione. Quindi, ogni slot verrà utilizzato per leggere via via i dati di ogni bitplane fino all’ultimo (l’ottavo), per poi ricominciare nuovamente.
E’ evidente come questo meccanismo degli slot cozzi terribilmente contro un possibile utilizzo per la grafica packed, che per definizione si trova tutta in sequenza in memoria e certamente non distribuita in 8 diverse zone di memoria. Infatti un sistema packed ha un solo puntatore alla memoria (al framebuffer) e il controllore video legge semplicemente uno dopo l’altro i dati che gli servono, senza ricorrere ad alcun arbitraggio degli accessi in memoria col meccanismo degli slot tipico del chipset Amiga.
I due meccanismi sono effettivamente inconciliabili se presi per quello che devono fare (implementare la pipeline necessaria a gestire lo specifico formato grafico), ma andando oltre questa rigida e schematica visione “o bianco o nero” è possibile pensare, invece, a un’alternativa che in qualche modo li renda compatibili, per lo meno per la finalità che ci si prefigge (esclusivamente quella di visualizzare la grafica di uno schermo packed, al minor costo possibile).
FrankenAmiga: innestare grafica packed in un “corpo” planare
L’idea che mi è venuta in mente (un po’ di anni fa, quando mi ponevo lo stesso problema) è quella di continuare a sfruttare i bitplane esattamente per come sono, in modo da non toccare tutto il complesso meccanismo degli slot. Quindi i dati degli 8 bitplane verranno prelevati sempre secondo lo stesso identico schema in uso nel chipset AGA, ma con la differenza che questa volta conterranno dati in formato packed (a 8 bit, ovviamente: un byte rappresenta l’indice del colore della tavolozza).
La differenza sostanziale sta nel come tali dati siano organizzati. O, per meglio dire, distribuiti negli 8 bitplane, perché questa è la chiave della soluzione al problema. Per essere più precisi, i primi byte della grafica packed si troveranno nel primo bitplane, i successi nel secondo, e così via fino agli ultimi che finiranno nell’ottavo bitplane.
Un esempio grafico servirà a chiarire la distribuzione dei pixel / byte meglio di un cumulo di parole, ponendo per semplicità che vengano caricati 16 bit alla volta (quindi due byte per ogni singolo bitplane):

Le lettere (A, B, C, …) sono utilizzate come “segnaposto” e soltanto per indicare il colore dello specifico pixel, ma penso sia abbastanza chiaro da questo diagramma quali byte / pixel del framebuffer / schermo finiscano nei rispettivi bitplane.
L’unico problema di quest’idea è che al momento non funzionerebbe correttamente e ciò perché il puntatore dello specifico bitplane viene incrementato della dimensione (in byte) ogni volta che il suo dato viene letto, in modo da essere pronto per poter leggere quelli dei successivi pixel da visualizzare. Nello specifico non funziona perché, ad esempio, dopo aver letto A e B, il bitplane #0 verrebbe incrementato di due e, quindi, i prossimi dati letti sarebbero C e D anziché Q ed R.
Questo succede perché i dati sono distribuiti su tutti e gli 8 bitplane, per cui la soluzione è molto semplice: coi dati packed bisogna incrementare ogni volta tenendo conto di tutti e 8 i bitplane. Dunque di 2 * 8 = 16 in questo caso. A questo punto si vede facilmente come, dopo aver letto A e B, se il bitplane #0 viene incrementato di 16 allora i prossimi dati letti, nel suo caso, saranno Q e R (17° e 18° byte), come atteso.
Quanto esposto sarebbe l’unica modifica da apportare al controllore dei canali DMA dell’Amiga. Considerando che con l’AGA si possono leggere dati a 16, 32, e 64 bit per ogni singolo bitplane, normalmente i bitplane vengono incrementati di 2, 4 e 8 byte rispettivamente. Abilitando la grafica packed dovrebbero essere incrementati, invece, di 16, 32 e 64 byte. Il seguente schema riassume tutto:
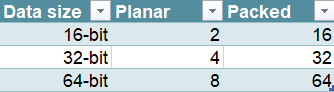
Anche l’implementazione risulta estremamente semplice nonché “economica”. La tabella che viene normalmente utilizzata internamente per la grafica planare andrebbe soltanto estesa tenendo conto del bit che abilita la grafica packed (il quale potrebbe trovare posto nel registro BPLCON0, che ha diversi bit liberi). Quindi bastano una manciata di transistor allo scopo, con un impatto del tutto trascurabile.
Il nuovo controllore video
Una volta prelevati i dati correttamente si pone il problema di estrarre i byte per ogni pixel da visualizzare e ciò richiede alcune modifiche importanti al controllore video, con la prima rappresentata dal fatto che abilitando il bit “Packed” in BPLCON0 (vedi sopra) si disabilita la logica planare (la quale prevede la combinazione di tutti i bit più significativi di ogni bitplane per formare l’indice, a 8 bit, del colore) e attiva quella packed, per l’appunto, che prevede semplicemente di estrarre gli 8 bit più significativi che sono stati letti per il bitplane #0 e utilizzarli immediatamente (non serve nessuna combinazione, infatti: gli 8 bit sono già a disposizione).
Gli 8 bit estratti serviranno poi per accedere alla tavolozza dei colori per prelevare le componenti cromatiche da inviare al monitor / TV, e ciò avviene esattamente come per la grafica planare.
Finito col primo pixel, si dovrà poi passare al secondo, poi al terzo, e così via, quindi serve scartare i dati del pixel visualizzato e preparare / posizionare opportunamente quelli del pixel successivo. Ciò richiede l’utilizzo di un barrel shifter, come abbiamo visto nei precedenti articoli sulla grafica packed. Specificamente, ne servirebbe uno da 64 bit (per gestire letture di dati di 64 bit alla volta) con un solo spostamento a sinistra di 8 posizioni, in modo da buttare via gli 8 bit già processati e muovere quelli del nuovo pixel nei bit significativi.
Il costo in termini di transistor è più elevato rispetto alla banale estrazione degli 8 bit più significativi (che ne richiede soltanto una manciata), ma ampiamente gestibile. Il problema sorge coi dati degli altri bitplane, perché finora abbiamo parlato esclusivamente di quelli del bitplane #0. Come fare a passare ai dati di bitplane #1 una volta finiti quelli di #0? In questo caso esistono due soluzioni abbastanza semplici, ma con costi diversi.
Aggiornamenti dati: prima soluzione
La prima, che richiede un costo più elevato, consiste nell’utilizzare 8 barrel shifter concatenati, in modo che quando si scarta il byte più significativo del bitplane #0 (ossia i dati del pixel appena processato) e si spostano di 8 posizioni a sinistra tutti gli altri bit, negli 8 bit meno significativi finiscano gli 8 più significativi di bitplane #1. Al contempo negli 8 bit meno significativi del bitplane #1 finiranno negli 8 più significativi del bitplane #2, e così via fino agli 8 bit meno significativi del bitplane #6 i quali finiranno negli 8 più significativi del bitplane #7. Quest’ultimo non avrà dati piazzati negli 8 bit meno significativi, perché non ci sono altri dati letti (tutti i dati dei bitplane verranno caricati nuovamente dalla memoria).
Un esempio in forma tabellare renderà più semplice la comprensione di questo meccanismo:
| Pixel | Bitplane #0 | Output | Bitplane #1 | Bitplane #2 | Bitplane #3 |
| 0 | AB | CD | EF | GH | |
| AB | A | CD | EF | GH | |
| B | CD | EF | GH | ||
| 1 | BC | DE | FG | HI | |
| BC | B | DE | FG | HI | |
| C | DE | FG | HI | ||
| 2 | CD | EF | GH | IJ |
Per semplicità ho riportato soltanto il contenuto dei primi 4 bitplane (ma la logica è esattamente la stessa anche tenendo degli altri 4), con l’aggiunta della colonna Output dove viene riportato l’indice del colore che è stato estratto dagli 8 bit più significativi del bitplane #0 (in modo da far vedere concretamente il risultato dell’elaborazione del pixel e cosa verrà utilizzato per accedere alla tabella della tavolozza dei colori).
La prima riga del primo pixel (il #0) è abbastanza semplice e riporta soltanto lo stato dei registri dati di tutti e quattro i bitplane.
La seconda riga mostra l’indice del colore estratto (A), che si trova, quindi, nella colonna Output.
La terza riga evidenzia l’eliminazione di tale indice dai dati del bitplane #0, che a questo punto rimane con un solo colore (B) memorizzato negli 8 bit più significativi.
La quarta riga (pixel #1) riporta lo spostamento a sinistra di 8 posizioni di tutti i dati dei bitplane. L’indice colore (C) che era presente negli 8 bit più significativi del bitplane successivo finiscono negli 8 bit meno significativi di quello attuale. Questo riflette lo stato del sistema, che adesso è pronto per l’elaborazione del secondo pixel.
Il funzionamento, come si può notare, è abbastanza semplice. E’ stato mostrato per letture in memoria di 16 bit, ma funziona esattamente allo stesso modo anche per letture di 32 o 64 bit (come avviene col chipset AGA).
Aggiornamenti dati: seconda soluzione
La seconda soluzione richiede l’uso di un solo barrel shifter a 64 bit con scostamento di 8 posizioni a sinistra, ma richiede un registro a 3 bit che indichi quale bitplane si stia attualmente processando (il #0, inizialmente). Man mano che i pixel sono processati e il registro dei dati del bitplane #0 viene shiftato a sinistra di 8 posizioni, negli 8 bit meno significativi non verrà inserito alcun dato (si possono inserire degli zeri).
Quando, però, tutti i byte del bitplane #0 sono stati processati, il relativo registro sarà ormai vuoto. In questo caso si incrementerà di uno il suddetto registro da 3 bit per “passare” al successivo bitplane (#1, poi #2, ecc.), si preleveranno i suoi dati, e si copieranno su quelli del bitplane #0. E così via, finché i dati di tutti e 8 bitplane saranno processati.
Anche qui, un esempio in forma tabellare servirà a dissipare ogni dubbio sul suo funzionamento:
| Pixel | Bitplane #0 | Output | # Pixels | Bitplane #1 | Bitplane #2 | Bitplane #3 | Bitplane counter |
| 0 | AB | 2 | CD | EF | GH | 0 | |
| AB | A | CD | EF | GH | |||
| B | 1 | CD | EF | GH | |||
| 1 | B | CD | EF | GH | |||
| B | B | CD | EF | GH | |||
| 0 | CD | EF | GH | ||||
| 2 | CD | 2 | CD | EF | GH | 1 | |
| CD | C | CD | EF | GH | |||
| D | 1 | CD | EF | GH | |||
| 3 | D | CD | EF | GH | |||
| D | D | CD | EF | GH | |||
| 0 | CD | EF | GH | ||||
| 4 | EF | 2 | CD | EF | GH | 2 |
Com’era prevedibile, il meccanismo risulta leggermente più complicato e vede l’introduzione dei due registri che tengono conto, rispettivamente, del numero di pixel contenuti nei dati del bitplane #0 (colonna # Pixels) e del bitplane attualmente in lavorazione (colonna Bitplane counter).
Il funzionamento rimane, comunque, molto simile al precedente meccanismo poiché, e come si può vedere, la parte del leone viene svolta sempre e comunque dai dati del bitplane #0.
La prima riga, che segna l’inizio dell’elaborazione (pixel #0), riporta lo stato del sistema. In questo caso è utile evidenziare come la nuova colonna # Pixels contenga il valore 2, il quale indica la presenza di due byte / indice colore nei dati del bitplane #0. Mentre la colonna Bitplane counter riporta 0, perché stiamo lavorando sul primo bitplane.
La seconda riga è identica a quella della precedente tabella, e mostra l’indice del colore estratto (A), che viene mostrato nella colonna Output.
Anche la terza riga è uguale a quella della precedente tabella, ma in aggiunta viene mostrato l’aggiornamento del numero di pixel disponibili (# Pixels), che da 2 passa a 1, in quanto un pixel è già stato processato e tolto di mezzo dai dati del bitplane #0
La quarta riga mostra già delle differenze significative, poiché nessun dato di tutti gli altri bitplane (#1, #2, #3) viene modificato, i quali rimangono, quindi, sempre gli stessi. bitplane #0, invece, si comporta esattamente come nella precedente tabella e, in generale, funziona sempre allo stesso modo.
Un’altra differenza significativa capita quando tutti i dati del bitplane #0 sono stati elaborati e, pertanto, non contiene più nulla (settima riga). A questo punto bisogna spostarsi a elaborare i dati del bitplane successivo (#1), come viene indicato dalla colonna Bitplane counter, che passa a indicare 1, per l’appunto. Inoltre i suoi dati (CD) vengono trasferiti in quelli del bitplane #0 e, al contempo, # Pixels viene impostato a 2 per evidenziare la presenza di due pixel da elaborare. Lo stesso meccanismo viene mostrato nella tredicesima riga, quando si dovrà passare a elaborare i dati del terzo bitplane (#2).
Costi implementativi
La prima implementazione, come già accennato, è la più costosa perché richiede l’uso di ben 8 barrel shifter a 64 bit con scostamento di 8 posizioni (ma ha anche il notevole vantaggio di essere estremamente semplice da realizzare: si piazzano i barrel shifter nel circuito e si collegano i dati/bit di tutti i bitplane al posto giusto).
Come abbiamo visto in un precedente articolo, un semplice barrel shifter a 8 bit con scorrimento singolo richiede circa 23 porte logiche, pari a 46 transistor. Per cui 8 barrel shifter a 64 bit richiederanno 46 * 64 = 2944 transistor.
La seconda soluzione è leggermente più complicata da implementare rispetto alla prima, ma ha il notevole pregio di richiedere pochissima logica / transistor allo scopo. I costi sono i seguenti:
- Servono 3 bit (3 celle SRAM) in un registro interno per indicare il numero di pixel rimanenti nel registro dati del
bitplane #0, quindi 3 x 6 = 18 transistor. - Per decrementare il numero di pixel rimanenti serve un sottrattore a 3 bit, che quindi deve far uso di 3 full-adder. Come abbiamo già visto, ogni full-adder richiede 9 transistor per la sua implementazione, per cui serviranno 3 x 9 = 27 transistor allo scopo.
- Servono altri 3 bit (3 celle SRAM) sempre in un registro interno per indicare su quale bitplane si sta lavorando, quindi altri 3 x 6 = 18 transistor.
- Anche qui, per passare al successivo bitplane su cui si sta lavorando servirà un sommatore a 3 bit, che richiederà 27 transistor.
- Infine, l’unico barrel shifter a 64 bit da singolo spostamento richiederà 46 x 8 = 368 transistor.
In totale questa soluzione richiederà 18 + 27 + 18 + 27 + 368 = 458 transistor.
Entrambe le soluzioni richiedono l’implementazione di:
- Estrazione degli 8 bit più significativi del registro dati del
bitplane #0. - Estensione della LUT (LookUp Table) utilizzata per indicare di quanti byte si deve incrementare il puntatore di ogni bitplane a seconda della dimensione dei dati da leggere in memoria. Una LUT viene implementata facendo uso di multiplexer (mux). Nello specifico, l’AGA richiede una LUT da 2 ingressi (che indicano la dimensione dei dati da leggere) e 4 uscite (che indicano di quanti byte si devono incrementare i bitplane). La nuova LUT richiederà, invece 3 ingressi (si deve tenere conto anche del bit “Packed“) e 7 uscite (per poter contenere il massimo valore: 64). Non mi è facile quantificare il numero di transistor, ma dovrebbe richiederne ben pochi, poiché in uscita abbiamo sempre una potenza del due.
- Serve della logica di bypass necessaria quando risulta attivato il bit “Packed“, poiché il controllore video deve scartare gli 8 bit elaborati se la grafica fosse planare e prendere, invece, gli 8 estratti dalla logica al primo punto. Si tratta anche qui di poca roba. Un mux 2-a-1 richiede 4 porte logiche per la sua implementazione e, quindi, 8 transistor. Quindi gli 8 mux 2-a-1 richiedono 8 x 8 = 64 transistor.
- Infine serve della logica di bypass per evitare di aggiornare i registri dati dei bitplane, che come sappiamo vengono shiftati di una posizione a sinistra ogni volta che un pixel viene visualizzato. Qui il costo è maggiore, perché servono 8 x 64 = 512 mux 2-a-1, per cui sono necessari ben 512 x 8 = 4096 transistor allo scopo.
Per confronto, l’implementazione di Akiko richiede almeno 8 registri a 32 bit che servono a contenere i dati di tutti i 32 pixel da convertire. Quindi serviranno 8 x 32 = 256 celle SDRAM, pari a 256 x 6 = 1536 transistor, ma il tutto senza tenere conto della logica necessaria a implementare la conversione chunky-to-planar di cui non ho schemi e, quindi, non è quantificabile in termini di transistor (ma che farebbe in ogni caso lievitarne il numero; anche se non è chiaro se possa arrivare vicino al budget della prima soluzione).
Com’è possibile vedere e a prescindere da quale delle due soluzioni adottare, il grosso del costo è rappresentato dalla logica di bypass per l’aggiornamento degli 8 registri dati dei bitplane, ma considerato che il solo chipset AGA ha richiesto circa un milione di transistor per la sua implementazione, l’aggiunta del supporto alla grafica packed a 8 bit risulta assolutamente fattibile.
Videogiochi (3D) con la nuova modalità packed
Quale che sia la soluzione adottata, l’importante è che il controllore video sia in grado di estrarre correttamente i dati packed e visualizzarli. Non serve, infatti, nient’altro allo scopo: l’implementazione per supportare dati packed è soltanto quella sopra esposta.
Rimane in piedi il problema di come i giochi 3D (ma anche 2D: in questo caso, però, sarà la CPU a occuparsi per lo più dell’aggiornamento della grafica) possano utilizzare questa nuova modalità video, ma sono necessari pochi cambiamenti, allo scopo, a livello di programmazione dei registri hardware.
Il primo è banale e riguarda l’attivazione del summenzionato bit “Packed” nel registro BPLCON0. Ovviamente il numero di bitplane dovrà continuare a essere impostato a 8 (anche se il framebuffer è uno soltanto: un’unica area di memoria che contiene tutti i dati), perché il gestore dei canali DMA deve comunque leggere i dati da tutti e 8 bitplane, come già spiegato all’inizio.
La seconda modifica riguarda, per l’appunto, i puntatori ai dati degli 8 bitplane. In questo caso soltanto il primo bitplane (#0) punterà all’inizio della prima riga del framebuffer. Mentre il bitplane successivo (#1) dovrà essere caricato con lo stesso indirizzo, ma con l’aggiunta della dimensione, in byte, dei dati da leggere (2 per 16 bit, 4 per 32 bit, e 8 per 64 bit), poiché i suoi dati si trovano immediatamente dopo quelli del primo bitplane. Il terzo bitplane (#2) che aggiungerà la stessa quantità all’indirizzo del secondo, e così via per tutti gli altri bitplane rimanenti. Se vi siete persi basterà rivedere velocemente la sezione “FrankenAmiga” e tutto tornerà chiaro.
Infine e ricordando che il controllore video dell’Amiga dispone di due registri, BPL1MOD e BPL2MOD, il cui valore viene aggiunto a tutti i bitplane dispari e pari, rispettivamente, alla fine dell’elaborazione di ogni riga (ciò serve per poter puntare correttamente a quella successiva), sarà sufficiente impostare entrambi a zero, in quanto tutti e 8 i puntatori ai bitplane risultano già puntare ai dati della riga successiva.
Quanto esposto attiene esclusivamente all’impostazione dei registri del controllore video in modo che possa correttamente visualizzare la grafica col nuovo formato packed / planare (considerato che, a tutti gli effetti, risulta un ibrido fra i due, da questo punto di vista).
A livello di programmazione vera e propria, ossia di accesso e manipolazione della grafica, tutto risulta semplificato perché il framebuffer è esattamente come ci si aspetta: un’area rettangolare in cui ogni riga è costituita da pixel i cui indici colore sono memorizzati in una sequenza di byte. Per cui si può operare esattamente come la famigerata modalità video 13h introdotta da IBM con la VGA dei suoi PC PS/2.
Conclusioni
Penso sia evidente di come le soluzioni proposte siano non soltanto fattibili (al posto di quella in Akiko), ma anche abbastanza semplici da realizzare, di gran lunga più efficienti (la grafica è già in formato packed e non richiede nessuna conversione, con relativa penalizzazione prestazionale) nonché molto più semplici da utilizzare per gli sviluppatori di videogiochi, con tutti i benefici che ne sarebbero derivati.
Gli ingegneri Commodore hanno implementato, invece, la soluzione in Akiko e ciò non per mancanza di tempo (visto che entrambe le soluzioni sono semplici) né tanto meno per il budget dei transistor (ne sono richiesti pochi in più, rispetto a tutti quelli che sono stati necessari per implementare l’intero chipset AGA).
L’idea che mi sono fatto è che si tratti di persone con scarsa creatività e ben poco “thinking out-of-order“, le quali hanno pensato di liquidare la questione con la prima cosa che gli è venuta in mente, senza spendere un po’ di tempo in più per pensare a qualcosa di meglio. D’altra parte la logica di conversione di Akiko è stata frutto di una chiacchierata a pranzo: cosa ci si poteva aspettare di più?
Probabilmente è gente abituata a ragionare poco e a risolvere con la forza bruta (“alziamo i numeri” per avere più banda, più colori, ecc.) anziché tirare fuori dal cappello qualcosa di originale e “migliore”. Né tanto meno hanno tenuto in debito conto di come funzionino i videogiochi e di come proporre soluzioni che ne avessero migliorato l’implementazione.
I frutti di tale mentalità li troviamo, ad esempio, nella progettazione dello stesso chipset AGA, dove sono stati semplicemente aumentati i numeri (2 e 4 volte la banda di memoria a disposizione per schermo e sprite, rispetto a OCS e OCS. 256 colori anziché 64) e null’altro.
Per essere ancora più chiari, noi programmatori ci siamo ritrovati con sprite la cui larghezza è passata da 16 a 32 pixel (con accessi a 32 bit alla Chip mem) o 64 pixel (accessi a 64 bit), ma sempre a 4 colori (16 colori soltanto appaiando due byte)! Una larghezza enorme, se teniamo conto che la risoluzione dello schermo utilizzata nei giochi è rimasta sempre la stessa (320 pixel in orizzontale) e, quindi, sprite enormi come quelli sarebbero stati di ben poca utilità.
Quando sarebbe stato di gran lunga più utile, invece, avere la possibilità di utilizzare per tutti e 8 gli sprite sempre 16 pixel orizzontalmente, ma con colori (accessi a 32 bit) oppure 256 colori (accessi a 64 bit), giusto per fare un esempio.
La Commodore ha avuto un gruppo manageriale a dir poco disastroso, come sappiamo, ma a mio avviso anche i suoi ingegneri non hanno certo brillato, “regalandoci” roba come l’AGA o, per l’appunto, il circuito chunky-to-planar in Akiko…









