
Dopo aver parlato dei giochi 2D veniamo, infine, a quelli 3D per “chiudere il cerchio”. I giochi AGA, che sono un argomento trasversale, verranno trattati a parte.
Non mi soffermerò in dettaglio su come funzioni il motore grafico di un gioco di questo tipo (anche perché non ne esiste uno soltanto, ma diversi, a seconda delle decisioni prese per certi aspetti, nonché le approssimazioni utilizzate), anche perché i concetti chiave si possono leggere ovunque (pure su Wikipedia).
Introduzione (molto veloce) alla rasterizzazione (3D -> 2D)
Ciò che è importante, ai fini di quest’articolo, è la fase finale del processo di generazione del fotogramma da visualizzare, che è chiamata rasterizzazione, cioè la conversione dei modelli 3D (usualmente costituiti da triangoli) che compongono la scena del gioco nello schermo 2D (chiamato framebuffer) che ne rappresenta la porzione / parte che verrà mostrata all’utente.

In particolare e una volta determinato che un triangolo (o parte di esso) rientri nella visuale (chiamata Picture Plane B nell’immagine qui sopra), ci si pone il problema di come disegnarlo nel framebuffer, assumendo di aver già effettuato tutti i calcoli (inclusa la rimozione delle facce nascoste) che ne hanno determinato gli equivalenti vertici in coordinate bidimensionali.
Rimane, insomma, da visualizzare il triangolo nello schermo (sto volutamente semplificando per non appesantire la discussione: l’immagine di cui sopra mostra come il triangolo rosso scuro non sia completo e, quindi, richiederebbe un trattamento particolare per essere correttamente visualizzato), fino a quando tutta la grafica dello schermo non sarà stata generata.
Operazione non semplice, in quanto l’Amiga non possiede hardware dedicato allo scopo, per cui o la CPU si fa carico anche (perché tutti i calcoli per aggiornare e gestire la scena sono soltanto suoi) dell’implementazione di questa primitiva grafica, oppure cerca di affidarsi in qualche modo al solito coprocessore che si occupa di manipolare la grafica: il Blitter.
Ovviamente la scelta più saggia sarebbe quella di impiegare il Blitter, poiché riesce a gestire la grafica di gran lunga più velocemente rispetto al processore (che sappiamo già essere abbastanza lento quando risultano coinvolti accessi alla memoria). Il problema è il come, perché questo coprocessore funziona con e gestisce soltanto aree rettangolari, le quali sono alquanto diverse dai triangoli.
Tracciare triangoli (pieni) col Blitter – Grafica planare
In aiuto arriva banalmente la geometria. I triangoli, infatti, sono costituiti da tre linee che racchiudono una superficie (piena). A questo punto e dopo esservi sorbiti questa tremenda sfilza di articoli molto tecnici, dovrebbe esser chiaro che queste cose siano fortunatamente appannaggio di questo coprocessore, come abbiamo visto principalmente nell’articolo dedicato al tracciamento delle linee e riempimento di aree (rettangolari).
La soluzione è, per l’appunto, semplice e immediata: basterebbe tracciare le due linee (bastano queste, anziché tutte e tre) che delimitano l’area del triangolo, ordinando successivamente al Blitter di utilizzare la funzionalità di riempimento di cui è stato dotato quando semplicemente si copia un’area di memoria (su un’altra. La quale potrebbe anche essere la medesima), prendendo come riferimento tutta l’area rettangolare che racchiuda quella del triangolo in oggetto.
Quindi e supponendo che i tre vertici del triangolo abbiano coordinate (x1, y1), (x2, y2), (x3, y3), sarà necessario:
- tracciare la linea (x1, y1) – (x2, y2);
- tracciare la linea (x2, y2) – (x3, y3). Ma questa si può tranquillamente evitare di disegnare;
- tracciare la linea (x3, y3) – (x1, y1);
- calcolare le coordinate minime e massime orizzontali. x_min = min(x1, x2, x3). x_max = max(x1, x2, x3);
- calcolare le coordinate minime e massime verticali. y_min = min(y1, y2, y3). y_max = max(y1, y2, y3);
- applicare la funzionalità di riempimento nell’area racchiusa da (x_min, y_min) – (x_max, y_max).
Ho deliberatamente evitato di parlare dei casi speciali (triangoli troppo piccoli, intersezione dei vertici) perché possono essere gestiti a parte, cosicché da concentrare l’attenzione sul caso più generale, in quanto è anche quello che porta via la stragrande maggioranza del tempo d’esecuzione & relative risorse (gli accessi alla memoria, che dominano su tutto).
L’algoritmo sopra esposto funziona, però, esclusivamente su un singolo bitplane. Sarà, dunque, necessario applicarlo a tutti i bitplane che compongono lo schermo, avendo cura di invertire il funzionamento nel caso i bit del particolare bitplane dovranno essere azzerati anziché impostati (a 1).
Per essere ancora più chiari, supponendo, ad esempio, di avere uno schermo con 16 colori (il quale richiede 4 bit per gli indici dei colori, con gli indici che vanno da 0 a 15) e nel caso in cui il triangolo da disegnare dovesse avere il colore 13 (equivalente a %1101 in binario), ciò vorrebbe dire che per il primo, terzo e quarto bitplane tutti i bit interessati dall’algoritmo di cui sopra dovranno essere impostati a 1, mentre ed esattamente al contrario dovranno essere a 0 tutti quelli del secondo bitplane (sempre e soltanto quelli coinvolti nell’operazione).
D’altra parte sappiamo bene, ormai, che questo è il prezzo da pagare con la grafica planare: ogni operazione (in genere. A meno dei casi speciali di cui abbiamo già parlato nei precedenti articoli) dev’essere ripetuta tante volte quant’è la profondità di colore dello schermo su cui si sta lavorando.
Per chiudere questa parte è necessario precisare che l’algoritmo su esposto si applica a un bitplane / buffer separato da quello dello schermo, che serve esclusivamente per tracciare il triangolo in tale buffer. L’area risultante sarà poi utilizzata con la primitiva cookie-cut per “incastrare” la grafica di tale triangolo nello schermo vero e proprio (un bitplane alla volta e come spiegato nell’esempio fornito), usando l’area che è stata tracciata contemporaneamente come maschera (per visualizzare la grafica del triangolo oppure quella dello schermo) e come dati della grafica.
Infine, l’area che è stata interessata in questo buffer addizionale dovrà essere azzerata (in modo da essere, quindi, pronti col successivo triangolo da elaborare), altrimenti l’algoritmo di riempimento del Blitter non funzionerebbe correttamente (troverebbe della grafica già presente, che lo porterebbe a generare artefatti).
Probabilmente altri sviluppatori di giochi avranno elaborato tecniche diverse, ma questa è quella che ho sempre pensato si potesse utilizzare per cercare di sfruttare il Blitter per la realizzazione di giochi 3D.
Tracciare triangoli (pieni) col Blitter – Grafica “packed” – Prima versione
Una prima implementazione per un possibile Amiga funzionante (soltanto) con grafica packed non sarebbe dissimile da quanto già esposto, ma con la differenza che, come visto nel pezzo che ha trattato le primitive grafiche di tracciamento linee e riempimento aree, servirebbe un ulteriore buffer costituito da una singola riga contenente lo specifico colore da utilizzare per disegnare il triangolo.
Tale riga dovrà avere la stessa larghezza dello schermo (e del buffer in cui si va a disegnare il triangolo “monocromatico”, col suddetto algoritmo). Come spiegato in precedenza, questo buffer aggiuntivo verrà utilizzato come una sorta di texture per mappare i pixel del triangolo col colore contenuto in tale riga. Ed è bene ribadire nuovamente che questo nuovo buffer sarà necessario esclusivamente per grafica avente una profondità di colore che non sia una potenza del due (quindi 8, 32, 64, 128 colori), altrimenti se ne potrà fare a meno e sarà sufficiente memorizzare il colore da utilizzare nell’apposito registro del Blitter (BLTBDAT).
Complessivamente il costo sarebbe leggermente superiore rispetto alla versione planare, poiché per ogni riga da elaborare sarà necessario leggere una volta in più la maschera.
Se, ad esempio, la grafica usa 8 colori, il triangolo risulta memorizzato in un’area larga 16 pixel, e ignorando al momento i problemi di allineamento, con la grafica planare sarebbero necessari 1 (lettura maschera = grafica del triangolo) + 1 (lettura fondale) + 1 (scrittura fondale) = 3 accessi in memoria per aggiornare lo schermo (quindi disegnandoci sopra il triangolo). Il tutto che va ripetuto per tre volte (i tre bitplane da aggiornare), quindi 3 x 3 = 9 accessi in memoria in totale.
Con la grafica packed, invece, sarebbero necessari 1 (lettura maschera = grafica del triangolo) + 3 (lettura della riga speciale col colore da applicare) + 3 (lettura fondale) + 3 (scrittura fondale) = 10 accessi in memoria. Quindi l’11% in più.
Tutto ciò, però, nel caso ideale = migliore, ossia dove la grafica da aggiornare risultasse perfettamente allineata. In realtà abbiamo visto che già coi videogiochi 2D la grafica packed consente di risparmiare parecchia banda (quindi accessi in memoria), e quella 3D non fa eccezione (anzi!). Quindi e a mio avviso, tale risparmio non soltanto consentirebbe di compensare quell’11% di perdita, ma finirebbe per ribaltare la situazione ponendo la grafica packed un po’ in vantaggio.
D’altra parte è ben noto, da tantissimo tempo, che il problema più grosso nei giochi 3D risieda nella banda di memoria, di cui sono a dir poco affamati, considerato l’enorme uso che se fa e che ha portato già da alcuni anni a misurarla in centinaia di GB al secondo nelle schede grafiche più moderne: molto più rispetto alla banda di memoria a disposizione per la CPU.
Com’è anche e altrettanto noto che la grafica planare risulti parecchio penalizzata per questo tipo di applicazioni. Eppure, e da quanto detto finora, non emergerebbe nulla che facesse pensare a un divario così marcato…
Tracciare triangoli (pieni) col Blitter – Grafica “packed” – Nuovo approccio
Per far portare in evidenza le differenze (che hanno poi portato velocemente all’abbandono della grafica planare) bisogna, infatti, cambiare radicalmente approccio, e lo si capisce bene guardando un qualunque esempio di rasterizzazione di un triangolo:

dove si può vedere come esistano due ampie parti dell’area rettangolare che racchiude il triangolo ma che a quest’ultimo non appartengono e, quindi, non devono essere disegnate. D’altra parte se dalla base si parte con tutti i pixel che devono essere tracciati, via via si arriva poi al vertice con un solo pixel di quella riga che risulta coinvolto nell’operazione.
Ciò che emerge, ed è questo il punto, è un consistente spreco di banda per tutte queste parti che non portano alcun contributo alla scena. Questo perché, con l’algoritmo sopra esposto, si rende necessario elaborare tutta l’area rettangolare, qualunque contenuto essa abbia.
A ciò bisogna aggiungere anche la questione dell’allineamento (orizzontalmente) della grafica a multipli di 16, poiché e come sappiamo la dimensione del bus dati è di 16 bit e, quindi, anche i bitplane dovranno essere processati con larghezze a essa congrue. Dunque l’area rettangolare da elaborare dovrà essere un multiplo di 16 orizzontalmente.
Ma un altro grosso problema è rappresentato dalla posizione orizzontale a partire dalla quale iniziare l’elaborazione del rettangolo: quando non è un multiplo di 16 (e ciò succede 15 volte su 16: praticamente sempre!) può portare all’allargamento dell’area interessata (come peraltro abbiamo già visto diverse e in particolare nell’articolo sui videogiochi 2D) con relativi accessi aggiuntivi in memoria.
La prima problematica (lo spreco dovuto alle aree non pertinenti al triangolo, come da immagine) può essere risolto cambiando completamente algoritmo e passando a uno che, anziché disegnare il triangolo sul buffer / bitplane addizionale per poi “sovraimporlo” (col classico cookie-cut) sullo schermo / framebuffer, vada a tracciare direttamente il triangolo sullo schermo, procedendo riga per riga.
Esistono diversi algoritmi allo scopo, ma uno molto famoso è quello di Bresenham, che fa uso dell’omonimo algoritmo per il tracciamento delle linee (di cui abbiamo parlato nel relativo pezzo), ma questa volta utilizzando due linee che tracciano i lati del triangolo come riferimento per procedere poi riga per riga, com’è possible comprendere meglio da un articolo che ne spiega il funzionamento.
Si tratta di un algoritmo che ovviamente si sposa benissimo con la grafica packed, riducendo al minimo i problemi di allineamento della memoria a 16-bit e ottimizzando al meglio gli accessi alla memoria e il relativo consumo di banda, specialmente all’aumentare della profondità di colore (perché si riduce il numero di pixel contenuti in una word = 16 bit).
Si potrebbe pensare di utilizzarlo anche con la grafica planare, in quanto tecnicamente non v’è nulla che lo impedisca, ma si perderebbe il vantaggio di programmare il Blitter una sola volta (per bitplane), come spiegato prima. Mentre col nuovo algoritmo questo coprocessore andrebbe programmato per ogni linea (magari fatta eccezione per i casi più semplici, come il tracciamento di uno o pochi pixel, a seconda della granularità determinata dalla profondità di colore).
Non avendo programmato giochi 3D (pur essendo comunque interessato all’argomento, in quanto sviluppatore di giochi per Amiga) non ho avuto il piacere di fare delle prove per vedere se si potessero ottenere vantaggi anche con la grafica planare usando l’algoritmo di Bresenham.
Ovviamente si potrebbero fare un po’ di calcoli prendendo l’esempio mostrato nell’immagine qui sopra e riportando i numeri per tutti i casi (planare con buffer & planare Bresenham, packed con versione ibrida & Bresenham) ma richiederebbe un po’ di tempo nonché considerazioni tecniche annesse, appesantendo di molto l’articolo. E questo tenendo conto soltanto del caso migliore (triangolo perfettamente allineato al buffer & framebuffer).
Per cui ho preferito evitare di ammorbarvi con un altro wall-of-text tecnico pieno di numeri (quando l’articolo, per sua definizione, è incentrato sui casi d’uso). D’altra parte non penso di proferire un’assurdità affermando che la grafica packed si presti meglio (e da sempre) per la grafica 3D, quindi non m’aspetto critiche almeno su questo punto.
Giochi con una sola tinta sui lati dei poligoni – Stunt Car Racer
Passando finalmente ai giochi, riporto alcuni esempi che usano la grafica 3D in modo diverso. Il primo, famosissimo titolo che ci ha regalato tante ore felici, è quel capolavoro di Stunt Car Racer:

che consente di esplicitare un paio di caratteristiche alquanto comuni (se non applicabili proprio a tutti i giochi).
Il primo è l’uso finestre / pannelli / cornici / oggetti che riducono effettivamente l’area in cui dovrà essere visualizzata la grafica 3D, in modo da ridurre il carico prestazionale da essa richiesto. Quindi lo schermo si presenta come un misto di grafica 3D e 2D, dove quest’ultima ha una parte rilevante.
In particolare Stunt Car Racer usa la grafica 3D per il cielo, il terreno, la pista ed, eventualmente, per l’auto avversaria (nei circuiti che la prevedono), lasciando il resto (nuvoloni di polvere, fiamme del motore, ecc.) alla grafica 2D.
Il motore 3D è, quindi, molto semplice (per lo meno questa è la mia percezione), focalizzato sostanzialmente sul tracciamento della pista e, quando presente, sull’auto avversaria (che è molto rozza e goffa, essendo costituita da pochissimi poligoni: le ruote sono addirittura quadrate!).
Inoltre, e come recita anche il titolo di questa parte, i poligoni disegnati fanno esclusivamente uso di singole tinte per le loro facce, com’è possibile visionare dalle schermate: c’è un solo colore che viene usato per riempire un determinato poligono.
Con ciò non intendo che venga usato un solo colore per tutta l’auto avversaria, ad esempio (la quale usa un rosso scuro e un rosa, com’è possibile vedere qui sopra), ma che un determinato poligono utilizzi un solo colore. Nello specifico, il retro dell’auto (che sarà costituito da un paio di triangoli) usa il rosso scuro, mentre i triangoli che compongono la carrozzeria utilizzano il rosa.
Probabilmente è per tutti questi motivi che il gioco risulta sufficientemente fluido da essere godibile perfino su un Amiga 500, anche se avrebbe potuto sicuramente guadagnare con la grafica packed in virtù delle considerazioni fatte sopra (molto meno spreco di banda di memoria).
Altro fattore comune è l’uso di grafica con soli 16 colori, che è sicuramente mortificante sapendo come l’Amiga sia in grado di visualizzarne 32 o addirittura 64, ma in questo caso si deve fare di necessità virtù, non per lo spazio occupato (il 3D è nato anche per ridurre considerevolmente le richieste di spazio occupato), quanto ed unicamente per risparmiare il più possibile la famigerata e onnipresente banda di memoria (di cui la grafica 3D è affamatissima consumatrice).
16 colori rappresentano, quindi, un buon compromesso fra varietà cromatica e prestazioni. Meno di 16 colori avrebbero certamente aiutato sul fronte puramente prestazionale, ma avrebbero appiattito troppo la grafica (8 colori per tutto sono veramente pochissimi) facendo alzare un grido corale di fantozziana memoria.
Tra l’altro sono molto interessanti per la grafica packed, perché si tratta di una potenza del due (richiedono 4 bit per essere memorizzati) e abbiamo visto come in questi casi i problemi dovuti alla dimensione del bus dati (16 bit) sono o inesistenti oppure estremamente ridotti. Tanta efficienza e comodità che consentirebbe perfino alla CPU di smazzarsi agevolmente parte del lavoro di rendering (almeno per i cosiddetti “corner case“: i casi particolari rappresentati da singoli o pochi pixel che rientrano tutti all’interno di una sola word).
Anche col Blitter se ne trarrebbe vantaggio, poiché si potrebbero precaricare i registri dei canali A e B rispettivamente con la maschera e il colore (o i colori. Come vedremo meglio dopo) se vogliamo che sia lui a gestire tutto (anche gli “spigoli” / pixel alle estremità delle linee da tracciare) in un colpo solo (con una sola operazione di blitting si può tracciare interamente una linea orizzontale appartenente al triangolo da disegnare / riempire).
Giochi con più tinte sui lati dei poligoni – Elite
Ciò ci porta dritti a un altro capolavoro assoluto, Elite:
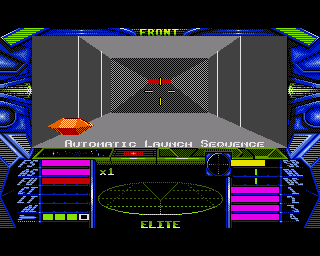
Sebbene non sviluppato originariamente per Amiga, il port per il nostro amatissimo computer è stato uno dei migliori.
Infatti, e nonostante sia stato rilasciato un anno prima di Stunt Car Racer, consentiva di utilizzare già una sorta di retino per “incrementare” il numero di colori visualizzati a schermo (quanto meno la percezione di usarne di più, grazie a questa tecnica), com’è possibile vedere dalla schermata qui sopra, simulando una tonalità più scura o più chiara del colore base mediante l’uso di retini neri o bianchi.
Ottenere l’effetto griglia comporta la suddivisione dell’area del poligono in coppie di righe, dove la prima riga inizia col colore base e a seguire con quello del retino (continuando poi quest’alternanza), mentre la seconda riga inizia col colore del retino e a seguire quello del colore base (e via con quest’alternanza), processando tutte le righe da riempire a due alla volta seguendo quest’algoritmo.
Questo comporta, usando il buffer aggiuntivo in cui tracciare inizialmente le linee del triangolo, la duplice programmazione del Blitter, dove la prima “passata” processa tutte le righe pari (ad esempio), mentre la seconda le righe dispari, provvedendo a utilizzare i colori giusti da impostare in modo da sfasare visivamente l’uso dei colori per riprodurre quel motivo.
Il costo di tale operazione non è, comunque, elevato. Inoltre l’area in cui riprodurre la grafica 3D in questo gioco è più piccola rispetto a Stunt Car Racer (come si può vedere confrontando le schermate), per cui complessivamente il risultato è accettabile (considerato l’hardware delle macchine dell’epoca).
In questo caso non riscontro differenze con una possibile implementazione packed, a parte che per il disegno di singoli puntini rappresentanti le stelle nello spazio, come pure gli spari, che essendo oggetti di piccole dimensioni, soprattutto orizzontalmente, sono molto più efficienti da disegnare perché in questo caso se ne può occupare tranquillamente anche la CPU (la grafica a 16 colori è molto più facile da manipolare, trattandosi di una potenza del due).
Sintesi Finale
Non credo ci sia altro da aggiungere perché i giochi 3D per Amiga rispecchiano più o meno tutti le caratteristiche di cui ho parlato finora (per quel che ricordo io, ovviamente).
Sappiamo che la grafica planare non è portata per questo tipo di giochi, mentre quella packed è più indicata (persino quando si tratta di utilizzare profondità di colore che non siano potenze del due).
Son cose che non scopriamo certamente con questo pezzo, che serve sostanzialmente a fornire una panoramica anche per questa tipologia. Il prossimo, che chiuderà questa miniserie, parlerà brevemente dell’AGA.









