
Dopo aver discusso dell’implementazione delle primitive grafiche più semplici passiamo a quella più complicata, ma che ha dato lustro al coprocessore per eccellenza presente nell’Amiga.
Il Blitter – inserimento di un oggetto grafico “mascherato” – Prima soluzione “packed“
Questa primitiva grafica è un’estensione nonché generalizzazione di quella trattata nel precedente articolo e consente di gestire i casi più complessi, come quello che capita nei videogiochi quando bisogna disegnare la grafica dei personaggi o dei vari oggetti che devono sovrapporsi alla grafica del fondale, quindi mostrando la grafica di tali oggetti quando non ci sono “buchi” e quella del fondale quando ci sono. Sostanzialmente è ciò che fanno gli sprite, ma il tutto dev’essere realizzato usando il Blitter.
La generalizzazione consiste nell’abilitare il DMA per il canale A, in modo tale che i dati letti siano usati come maschera per decidere, per ogni singolo bit, se inviare alla destinazione il bit della sorgente B (ad esempio quando il relativo bit della maschera sia zero) o quello della sorgente C (quando il relativo bit della maschera sia uno), supponendo che la sorgente B contenga la grafica di un oggetto mentre la C quella del fondale (che è anche lo schermo visualizzato, alla fine).
Tutto funziona liscio con la grafica planare (e, fino a prima di questa primitiva grafica, funzionava benissimo anche con quella packed), ma il grosso problema adesso è che, sì: la profondità di colore conta, eccome!
Infatti una prima soluzione al problema è banale ed economicissima in termini di implementazione hardware, in quanto e ancora una volta… non richiede nessuna modifica al Blitter, che rimane esattamente così com’è. Ma il prezzo da pagare in questo caso è salatissimo in termini di spazio occupato. Infatti la soluzione è che la maschera sia costituita da tanti bit quanti siano quelli usati per l’indice dei colori dei pixel, avendoli tutti a uno (ad esempio) per indicare che i relativi bit dell’oggetto debbano essere copiati e tutti zero altrimenti (debba essere copiata la grafica del fondale).
Inutile dire che lo spazio occupato letteralmente esploda all’aumentare della profondità di colore, mentre con la grafica planare la maschera ha sempre la stessa profondità di colore (un bit per pixel), qualunque sia il numero di bitplane utilizzati. Per cui e pur essendo una soluzione che dimostra senza dubbio la validità della tesi, alla fine non è concretamente adoperabile considerata la poca memoria a disposizione all’epoca dell’introduzione dell’Amiga.
Il Blitter – inserimento di un oggetto grafico “mascherato” – Seconda (buona) soluzione “packed“
Quella che consente di risolvere questo problema (tra l’altro ottimizzando l’uso della maschera, la quale viene caricata una sola volta, a prescindere dalla profondità di colore) è più complicata (come peraltro avevo già annunciato nell’articolo teorico su grafica planare vs packed) e prende in prestito, per una sua parte, l’algoritmo che ho illustrato per il nuovo controllore video.
L’idea, a grandi linee (più avanti passerò ai dettagli implementativi) consiste nel prelevare i dati della maschera facendo sempre uso del canale A. Ricordo che i singoli bit decidono se utilizzare il colore della sorgente B o della sorgente C. Il problema è che i colori sono memorizzati come informazione packed, per l’appunto, che peraltro ha una dimensione variabile: la profondità di colore varia da 1 a 6 bit (per OCS/ECS. Fino a 8 per AGA). Al momento concentriamoci su OCS/ECS, e specificamente soltanto su profondità di colore da 2 a 6 bit per pixel, poiché per il caso di un solo bit il Blitter funziona già così e non è necessario tenere conto anche di questo caso nell’implementazione della nuova soluzione.
Per quanto visto nel precedente articolo (nella sezione “Spostare una porzione rettangolare“) e con la precedente soluzione (che richiede uno spazio enorme), servirebbe che la maschera fosse costituita, invece, da tanti bit (tutti a zero o tutti a uno) quanta sia la profondità di colore, per ogni pixel da processare. La trovata, pertanto, consiste nello “espandere” un singolo bit che si trova nel registro dati del canale A per il numero di bit della profondità di colore.
Dunque se il bit più significativo (#15) (ricordo che si parte sempre da questo nelle elaborazioni con l’Amiga, perché è big-endian) risulta 1, allora dovrà generare tre bit (rimaniamo sempre nell’esempio di uno schermo a 8 colori) tutti a 1: 111. Se il bit successivo (#14) è 0, dovrà generare altri 3 bit, ma a 0 questa volta: 000. E così via, finché non si riempie almeno una word (16-bit) da poter essere utilizzata come maschera / dato da combinare con le word lette per i canali B e C, e generare finalmente la word che andrà a finire nel canale D (quindi in memoria).
Tutto fila liscio per profondità di colore che siano potenze di due, perché consentono di generare sempre maschere da 16-bit coi bit letti dal canale A, ma per le profondità di colore che non lo siano ci sarebbero problemi (c’era da aspettarselo), poiché i bit generati sarebbero sempre o meno di 16 o più di 16 bit: non si scappa! La seguente tabella mostra la situazione precisa, per ogni profondità di colore:
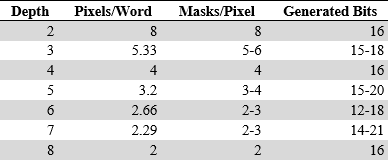
E’ possibile vedere come i casi con profondità di colore non potenze di due siano in grado di generare maschere diverse, a seconda del numero di bit utilizzati dalla sorgente A. Nel caso che stiamo considerando, quindi 3 bit per indice colore, vengono generate maschere di 15 bit utilizzando 5 bit dalla sorgente A, oppure di 18 bit con 6 bit usati. A seconda del momento servirà, quindi, generare maschere a 15 o 18 bit, combinandole con eventuali bit rimasti dalla precedente generazione, in modo da avere sempre a disposizione almeno 16 bit da combinare con gli altrettanti delle sorgenti B e C.
Il concetto che sta alla base del nuovo algoritmo che ho realizzato (ancora una volta, non so se altri abbiano già pensato e/o realizzato qualcosa di simile: l’importante è che abbia trovato io una soluzione al mio problema) è, quindi, di:
- generare al volo una nuova maschera richiesta a partire da alcuni dati presi dalla sorgente A, da combinare con eventuali bit della maschera che era stata precedentemente generata;
- utilizzare, allo scopo, il minor numero di bit richiesti dalla sorgente A se, tenuto conto dei bit rimasti, il totale sia sufficiente a ottenere una maschera finale di almeno 16 bit;
- combinare i bit rimasti con quelli nuovi che sono stati generati (i quali seguono quelli rimasti: finiscono sempre in coda, nei bit meno significativi);
- copiare i 16 bit più significativi di tale maschera (inviandoli alla sezione di elaborazione che si occupa di combinarli con quelli delle sorgenti B e C);
- togliere di mezzo i suddetti 16 bit e spostare i rimanenti (se ci sono) nei bit più significativi della maschera generata;
- aggiornare il numero di bit a disposizione nella maschera generata con quelli che sono rimasti;
- eliminare i bit utilizzati dalla sorgente A e aggiornarla di conseguenza.
Quest’ultimo punto ricalca esattamente quanto è stato già illustrato nel secondo e terzo articolo (quelli relativi al nuovo controllore video packed, che spiegano i nuovi concetti di buffer, byte interno, e primo byte della coda FIFO), per cui non fornirò ulteriori spiegazioni, a parte precisare che, in questo caso, il registro interno del Blitter che viene usato per conservare i dati letti dalla sorgente A (BLT1DAT) viene, per l’appunto, suddiviso in 8 bit per il Buffer e 8 bit per il Byte Interno, oltre al fatto che gli viene associata una coda FIFO (di soli due elementi).
Il Blitter – inserimento di un oggetto grafico “mascherato” – Un esempio
Come in precedenza e per cercare di aiutare nella comprensione di questo nuovo meccanismo, di seguito fornisco un esempio sotto formare tabellare che mostra esattamente quanto sopra esposto.
La colonna Word indica a quale word a 16-bit della sorgente A il (nuovo) Blitter sta lavorando per generare la maschera a 16-bit richiesta (0 indica la prima word / maschera, 1 la seconda, e così via).
Le colonne Buffer A, Bits, Int. Byte, Bits e First Byte FIFO assumono lo stesso significato di quanto visto in precedenza (il primo Bits è Bits in Buffer, mentre il secondo è Bits in Int. Byte) per il nuovo controllore video, con in aggiunta Total che corrisponde alla somma delle due colonne Bits (serve a rendere meglio l’idea di quanti bit siano rimasti nella sorgente A, per generare maschere).
Full mask generated viene usata per mostrare, rispettivamente, i bit rimasti dalla precedente maschera, i (soli) bit che sono stati generati per la nuova maschera, e infine la combinazione dei bit rimasti e di quelli che sono stati generati. Questa suddivisione d’utilizzo temporale di questa colonna avviene per scopo esclusivamente esemplificativo: per meglio evidenziare i meccanismi interni che portano alla generazione finale della maschera che sarà poi utilizzata. Similmente avviene per la seguente colonna Bits, la quale illustra il numero di bit presenti nella precedente colonna / registro interno, a seconda dello specifico momento.
Infine Used mask mostra i 16 bit che sono stati estratti dalla maschera generata, per essere poi combinati con gli equivalenti delle sorgenti B e C.
Adesso risulta più facile capire il significato delle righe (a parte la prima, dopo quella d’intestazione, che riporta semplicemente l’ordine dei bit contenuti nella colonna) della tabella con gli esempi (i letterali, al solito, sono utilizzati per identificare i bit presenti in quella posizione, ma di cui non c’interessa conoscere il valore):
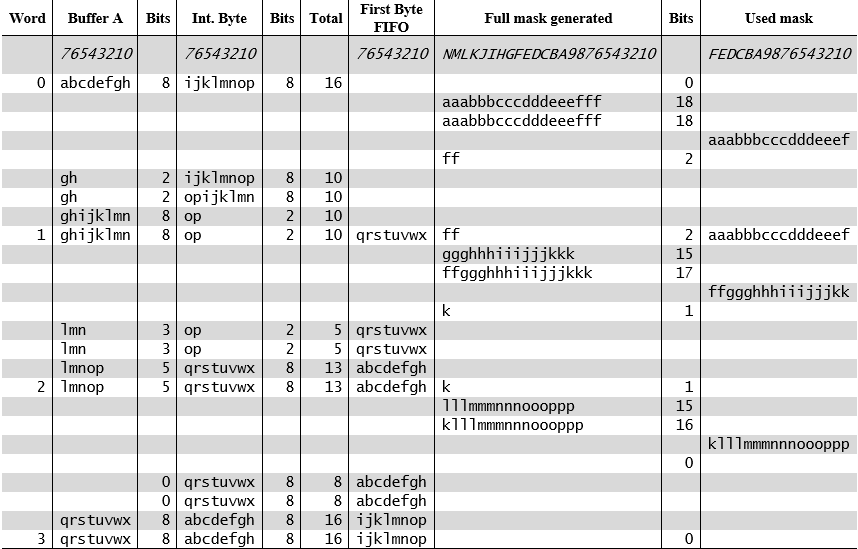
Per ogni word processata per la sorgente A sono presenti 8 righe:
- la prima riporta lo stato completo all’inizio dell’elaborazione;
- le successive cinque mostrano le operazioni interne che portano alla generazione della maschera e a quella da 16-bit che verrà inviata per essere combinata con le sorgenti B e C;
- le ultime tre riportano l’aggiornamento del buffer della sorgente A (con annessi byte interno e coda FIFO).
Partendo dalla prima riga (Word #0), vediamo come il buffer per la sorgente A risulti pieno (8 bit) come pure il suo byte interno, per un totale di 16 bit. La maschera generata (in precedenza) è, invece, completamente vuota (come riporta anche la sua colonna Bits: 0 bit) e non ne è stata usata nessuna parte (anche Used mask è vuota).
A questo punto il Blitter deve decidere se prelevare 5 o 6 bit dal buffer per generare una maschera di 15 o 18 bit (ricordo che l’esempio è per grafica a 8 colori = 3 bit usati per l’indice del colore del pixel). Poiché la maschera generata non ha alcun bit (0), deve optare per la seconda possibilità. Dunque preleva i 6 bit più significativi del buffer (abcdef) e li usa per generare la nuova maschera (aaabbbcccdddeeefff), che appare nella seconda riga. Infatti Full mask generated mostra, adesso, 18 bit , com’è anche riportato dalla sua colonna Bits.
La terza riga (ricordo sempre che partiamo dalla Word #0) è identica alla seconda, perché non ci sono bit rimasti dalla precedente maschera generata, per cui non c’è niente da combinare con la nuova maschera, e il risultato coincide con quest’ultima.
Con la quarta riga possiamo finalmente vedere come i 16 bit da combinare coi rispettivi delle sorgenti B e C siano pronti, come evidenziato dalla loro presenza nella colonna Used mask. Ovviamente si tratta dei 16 bit più significativi presenti in Full mask generated.
Una volta copiati devono essere rimossi e questo, infatti, è ciò che viene mostrato nella quinta riga, la quale riporta la presenza dei due soli bit rimasti (ff) nella medesima colonna, oltre all’aggiornamento dell’associata colonna Bits (che adesso riporta il valore 2).
A questo punto il lavoro svolto dal nuovo algoritmo di generazione automatica delle maschere è sostanzialmente finito, ma per completare il tutto bisogna togliere dal buffer i bit che sono stati utilizzati (abcdef) e rimpiazzarli prendendoli (sono ijklmn. Ma verranno inseriti in coda ai bit rimasti nel buffer, che infatti conterrà poi ghijklmn) dal byte interno (in cui rimarranno, poi, soltanto due bit: op). Questo lavoro è svolto dal nuovo algoritmo che è stato già presentato per il controllore video packed e l’esempio fornito ne mostra dettagliatamente il funzionamento.
Tutto ciò è esposto nelle ultime tre righe (dalla sesta all’ottava) della Word #0, le quali mostrano fedelmente le operazioni interne che conducono allo stato conclusivo, com’è infine riportato nella prima riga della Word #1 (che include anche i cambiamenti apportati dalle prime cinque righe).
La second Word (#1) è interessante perché mostra come questa volta il Blitter preleverà soltanto 5 bit per generare la maschera (di 15 bit, adesso: ggghhhiiijjjkkk), poiché quelli rimasti dalla precedente (due: ff) sono sufficienti (2 + 15 = 17) per i 16-bit che sono necessari (ffggghhhiiijjjkk), lasciando un solo bit residuo (k) per la successiva Word (#2). Mostra, inoltre, come il byte interno si svuoti completamente, per cui viene ricopiato in esso il primo byte della coda FIFO a esso associata (qrstuvwx) mentre verrà poi caricato in quest’ultimo l’altro byte (abcdefgh).
Infine la terza Word (#2) chiude il cerchio, poiché anche in questo caso vengono prelevati 5 bit (lmnop) e generata una maschera di 15 bit (lllmmmnnnoooppp), ma adesso nella precedente maschera è rimasto un solo bit (k) e, dunque, risulteranno presenti esattamente i 16 bit necessari (klllmmmnnnoooppp), lasciando Full mask generated completamente vuota stavolta. Anche il buffer si svuota completamente, per cui in esso verrà integralmente copiato il byte interno (qrstuvwx), che a sua volta verrà rimpiazzato dal primo byte della coda FIFO (abcdefgh).
L’inizio della quarta Word (#3) mostra uno scenario estremamente simile al primo, in quanto buffer e byte interno sono pieni (come pure la coda FIFO), col resto che è tutto vuoto. Il che è anche normale nonché atteso, perché con profondità di colore di 3 bit il processo di generazione delle maschere è ciclico (si ripete sempre allo stesso modo) e torna allo stato iniziale ogni 3 word elaborate. Altre profondità di colore hanno cicli simili, che si ripeteranno in base al numero di bit usati per gli indici del colore.
Concluso l’esempio, il prossimo pezzo si concentrerà sul meccanismo di generazione delle maschere, i costi implementativi del nuovo algoritmo, e il funzionamento per l’AGA.









