Nello scorso articolo abbiamo visto perchè la Branch Prediction è una componente essenziale dei processori superscalari, da quali blocchi base è composta e come questi blocchi si raccordano col resto dell’architettura. Adesso bisogna rispondere all’ultima domanda: che cosa c’è davvero dentro un predittore dinamico? Che algoritmi vengono usati per generare le predizioni?
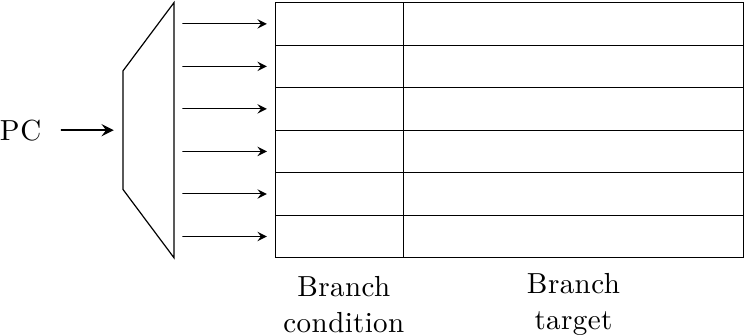
Innanzitutto, il predittore deve predire due cose contemporaneamente: la direzione di salto e, se il salto è preso, il bersaglio di salto. Un termine comune trovato in letteratura per questo tipo di struttura è Branch Target Buffer (BTB) e ha quest’aspetto:
E’ simile ad una piccola cache, indirizzata tramite il Program Counter, che restituisce la direzione di salto (basata in qualche modo sulla storia passata di quel salto) e il bersaglio di salto (l’indirizzo a cui si è saltati l’ultima volta che il salto è stato eseguito).
Come per ogni cache, anche per questa ci sono due requisiti contrastanti:
- velocità: idealmente vorremmo che il BTB risponda in un solo ciclo di clock, in modo da avere una predizione per il prossimo PC dato il PC corrente; memorie veloci devono essere piccole (più la memoria è piccola più le interconnessioni sono brevi e la circuiteria è semplice, riducendo il tempo di accesso)
- hit rate: il tasso di predizione corretta è in realtà il prodotto di due fattori: il tasso di predizione del BTB per lo hit rate del BTB, cioè quanto spesso troviamo nel BTB le informazioni che stiamo cercando; idealmente vorremmo avere uno hit rate del 100%, che impone l’uso di BTB grossi
Anche il tipo di associatività è importante: una cache fully-associative avrà uno hit rate maggiore, ma sarà più lenta; il contrario è vero per una cache direct mapped. Tutti questi fattori sono critici nella progettazione del predittore e vengono estensivamente analizzati con simulatori architetturali.
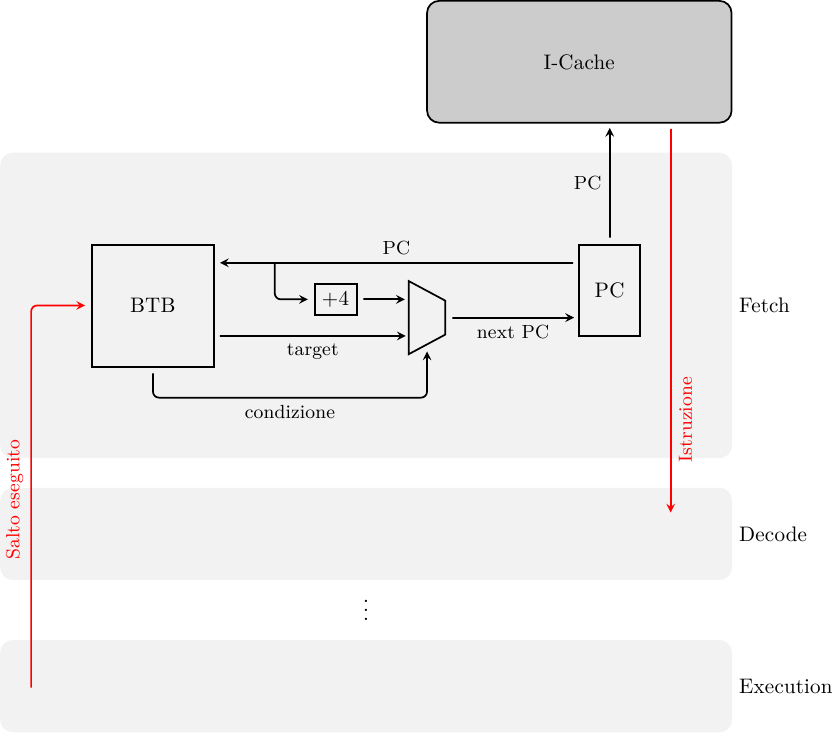
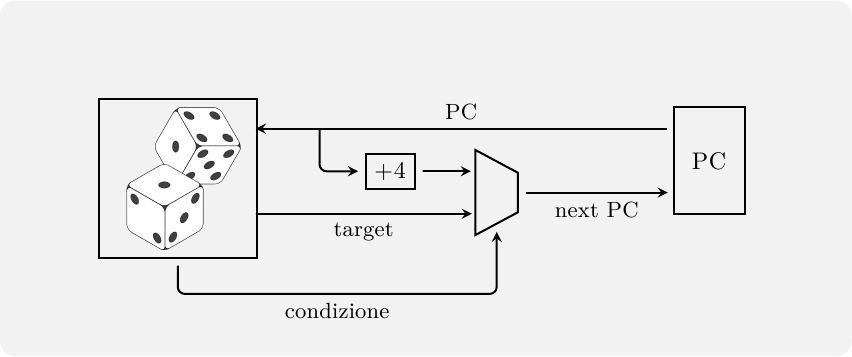
Il Program Counter corrente viene usato quindi per accedere contemporamente alla Instruction Cache e al predittore, per ottenere il prossimo PC. Lo stadio di Fetch assomiglierà allora a qualcosa del genere:
Supponendo di avere un processore RISC con istruzioni a 32 bit, il prossimo PC sarà o il PC corrente più 4 byte (se il BTB predice salto non preso, o se si è verificato un miss) oppure il PC contenuto nel BTB stesso (se cè stato hit nel BTB ed è stato predetto salto preso). Se la predizione è corretta, e l’indirizzo bersaglio è disponibile al prossimo ciclo di clock, la penalità di salto è stata completamente cancellata: il salto dovrà comunque essere eseguito per la validazione della predizione, ma potrà essere eseguito in parallelo con le istruzioni che lo seguono, invece che prima di esse. Questa è la “magia” della Branch Prediction.
Usare il passato per predire il futuro
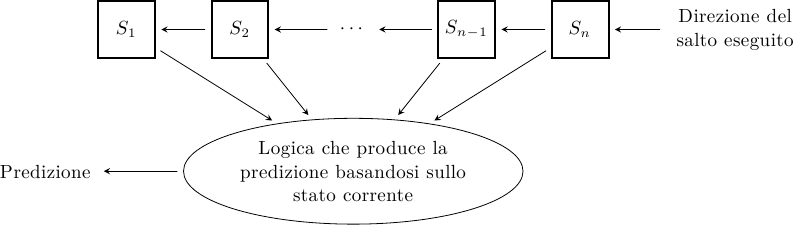
Il modo più semplice per predire la direzione di salto è costruire una macchina a stati finiti (FSM) che tiene traccia degli ultimi N esiti del salto (1 bit per esito): la macchina avrà 2^N stati, e ad ogni stato è associata una predizione:
Studi sperimentali dimostrano che è sufficiente un numero molto piccolo di bit per avere ottime prestazioni: 2 bit sono già sufficienti a superare il 90% di predizioni corrette nella maggior parte dei casi.
Il sistema più semplice è tenere 1 solo bit di storia per salto, cioè predire per il prossimo salto la stessa direzione di quello precedente. Sembra quasi uno scherzo, un sistema così semplice non può essere accurato! Invece, dal momento che la maggior parte dei salti è fortemente polarizzata, perfino con un solo bit di storia è facile ottenere predizioni accurate a più dell’80% !
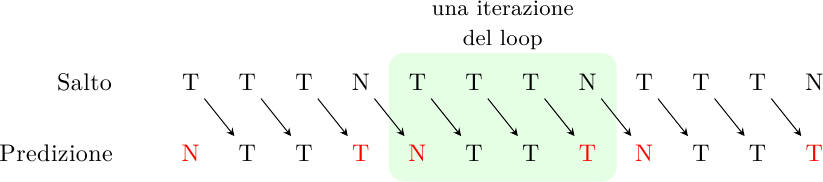
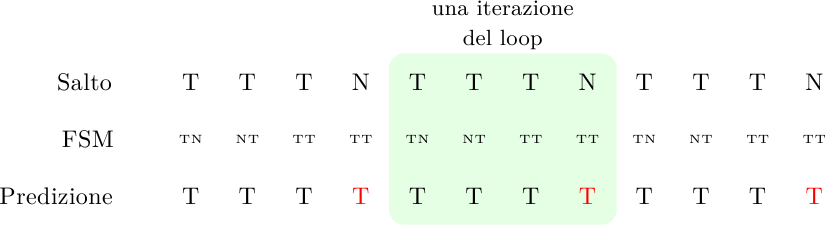
Uno dei casi più comuni di salti sono quelli che controllano la condizione di uscita da un loop. Come si comporta un predittore a 1 bit in questo caso? Supponiamo di avere un piccolo loop che si ripete 4 volte, il meccanismo allora funzionerà così:
dove ho indicato in rosso le predizioni errate. Il predittore indovinerà appena il 50% delle volte. In generale, sbaglierà sempre la prima e l’ultima iterazione del ciclo. Per cicli lunghi questo non è grosso problema, ma per cicli brevi l’accuratezza cade a livelli inaccettabili.
Come si comporta in questo caso un predittore a 2 bit, cioè un predittore che tiene traccia degli ultimi due esiti di ogni salto? Prima di tutto bisogna rispondere alla domanda: quale predittore a 2 bit? Con 2 bit si può costruire una FSM a 4 stati, e ci sono molti modi di collegare quegli stati… infatti, ce ne sono più di 4 milioni!
Il conto si fa così: da ogni stato escono due transizioni, una per quando il salto è preso (taken) e una per quando non è preso (non-taken); ogni transizione può andare a finire in ognuno dei 4 stati della FSM, quindi ci sono 4 * 4 = 16 possibili combinazioni di transizioni per stato, e 16 ^ 4 = 65536 possibili tabelle di transizione per l’intera macchina. Inoltre, ogni stato può generare una predizione preso/non preso, che genera ulteriori 2 ^ 4 possibilità. Per finire lo stato iniziale può essere uno qualunque dei 4 stati. In totale, ci sono 65536 * 16 * 4 = 4194304 possibili predittori a 2 bit!
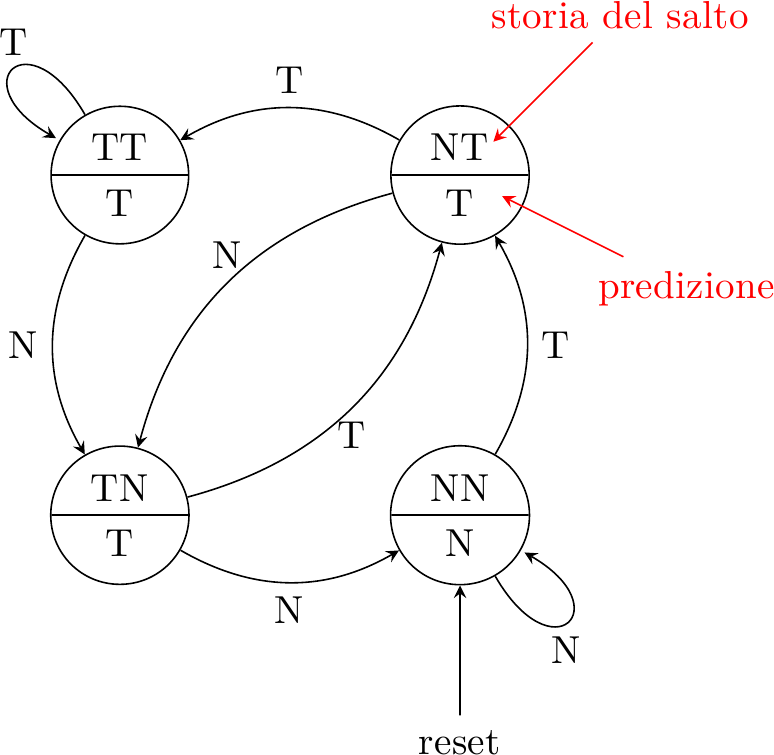
Naturalmente la quasi totalità di questi predittori è completamente inutile, ma esiste un piccolo numero di soluzioni alternative con buone caratteristiche. Uno studio sperimentale esaustivo fu condotto nel 1992 da Ravi Nair per IBM. Con poca sorpresa, il predittore migliore si rivelò essere anche quello più ovvio da immaginare: un contatore a saturazione, originariamente proposto da Jim Smith all’inizio degli anni ’80 e brevettato per la CDC:
Il predittore predice un salto preso in 3 stati su 4: solo se gli ultimi due esiti sono stati non-preso, allora predirà non-preso. Confrontiamo il comportamento di questo predittore con quello del predittore a 1 bit, sullo stesso loop:
Il predittore predice di prendere sempre il salto! Questo è un miglioramento rispetto al caso precedente, perchè ora si sbaglia solo l’ultima iterazione del ciclo e basta. Nel caso di loop a 4 iterazioni, la percentuale di successo sale dal 50% al 75%, un ottimo incremento.
E se aumentassimo il numero di bit di storia, otterremmo risultati migliori? Sì, ma non molto. Un altro studio sempre di Nair misurò sperimentalemente questi valori:
1 bit: 82.5% - 96.2% 2 bit: 86.8% - 97.0% 3 bit: 88.3% - 97.0%
Passare da 2 a 3 bit, nei casi da lui considerati, aumentava di poco il caso peggiore, e per nulla il caso migliore, e tutto questo usando il 50% di bit in più, che significa buffer più grosso e quindi più lento: è addirittura possibile che, una volta tenuta in conto l’implementazione circuitale, il sistema a 3 bit sia più lento!
Per fare un salto in avanti e costruire predittori molto più efficaci bisogna pensare a qualcosa di molto diverso… e molto più sofisticato.
Predittori a due livelli
Fino a questo momento abbiamo considerato ogni branch a sè stante, scollegato dagli altri branch del programma, ma l’esperienza ci dice che spesso l’esito di un branch dipende da quelli dei branch vicini a lui, oppure dall’esito passato del branch stesso, ma tenendo in considerazione non il mero numero di salti presi/non presi, ma la loro sequenza temporale.
Ad esempio, nel loop degli esempi precedenti, sappiamo che se abbiamo preso il salto 3 volte di fila, allora la prossima volta sarà non preso, altrimenti sarà preso.
Un esempio di correlazione “spaziale” (tra branch vicini) invece potrebbe essere:
int x, y, z;
...
if( x == 0 ) {
z = 0;
}
...
if( x * y > 4 ) {
...
}
...
if( z < 2 ) {
...
}
Se il primo salto è non-preso (cioè l’if è vero e viene eseguito il codice tra parentesi, immediatamente seguente al branch) allora sicuramente il secondo salto è preso e il terzo è non-preso. Se riuscissimo a correlare tra loro questi salti, una volta eseguito il primo, se esso fosse preso sapremmo come eseguire gli altri due con una affidabilità del 100% !
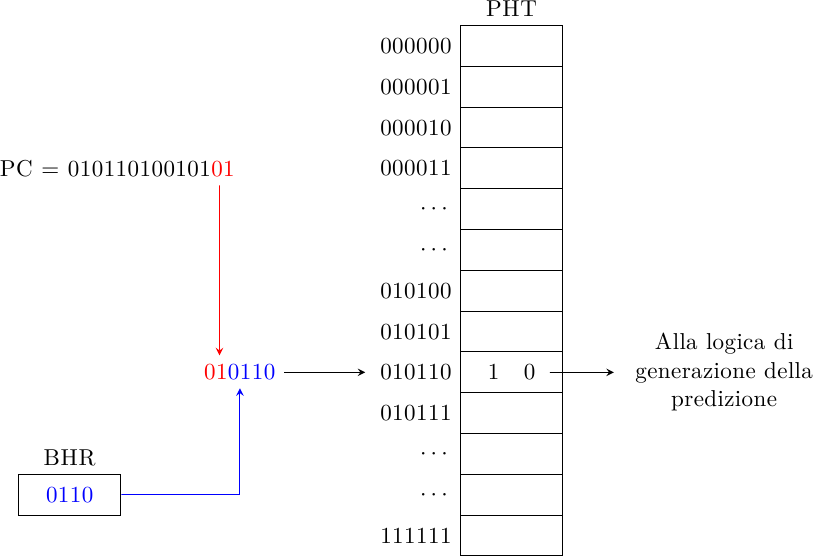
All’inizio degli anni ’90 due ricercatori (Yeh e Patt) proposero una famiglia di predittori basati su due livelli: il primo livello tiene traccia della storia dei branch eseguiti prima di quello in esame (cioè dei branch vicini nel codice, eseguiti appena prima di questo), mentre il secondo è una tavola di contatori a 2 bit (gli stessi visti prima), che tiene traccia della storia del salto in esame:
Il Branch History Register (BHR) è uno shift register dove vengono accumulati i risultati degli ultimi N branch (qualunque essi siano). Il BHR tiene traccia quindi della storia globale, il percorso di istruzioni che ci ha portati al salto in esame; la Pattern History Table (PHT) è una collezione di predittori indicizzata tramite una concatenazione della storia globale con (una parte del) l’indirizzo del salto in esame: in questo modo è possibile fare predizioni diverse per lo stesso salto a seconda del code path che ci ha portati lì. Questo schema è chiamato Global History 2-Level Predictor.
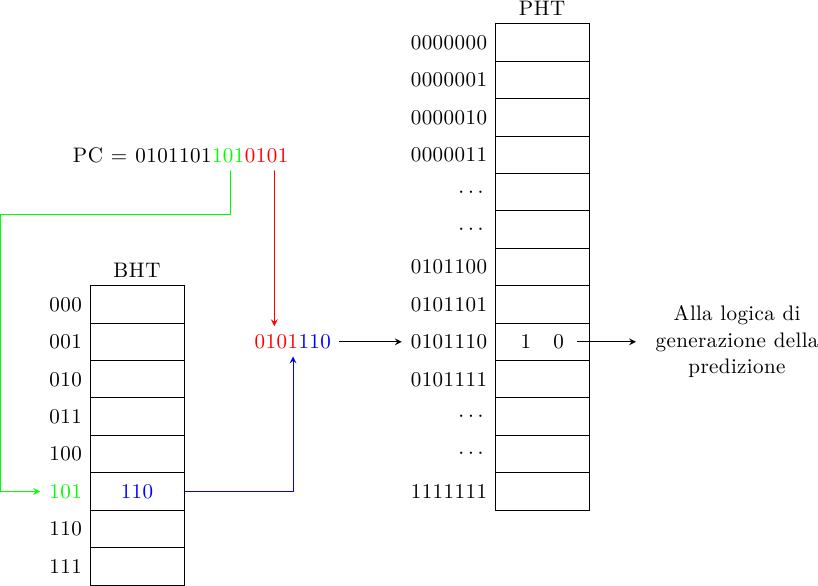
Uno schema simile (sempre di Yeh e Patt) è il Local History 2-Level Predictor:
In questo caso ogni branch ha il suo shift-register (Branch History Table) e tiene traccia della propria storia separatamente da quella degli altri branch (da cui il nome local). Di nuovo, la storia del salto viene concatenata all’indirizzo del salto stesso per accedere alla PHT e generare la predizione. Lo schema Global History può essere considerato un caso particolare di questo, dove la BHT ha una sola cella (in altre parole, zero bit sono necessari per accedere alla BHT).
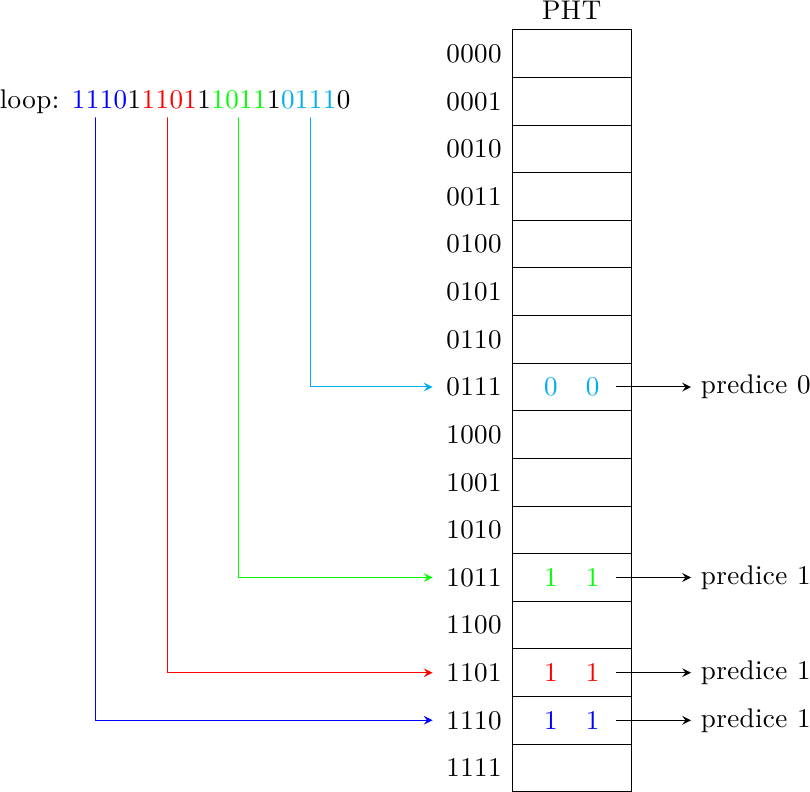
Torniamo all’esempio del loop con 4 iterazioni: come si comporta un Local History Predictor in questo caso? Finalmente abbiamo uno schema capace di fare predizioni diverse a seconda della diversa storia del salto, quindi ci aspettiamo che sia capace di fare meglio degli algoritmi precedenti, che erano invece costretti ad eseguire una “media” della storia del salto. Questo è infatti il caso:
dove ho indicato con ‘1’ un salto preso e con ‘0’ un salto non preso: si alternano successivamente tre 1 e uno 0. Dopo un certo numero di ripetizioni del loop, il predittore ha imparato che se la storia locale contiene un salto non preso e tre presi il prossimo sarà non preso, e sarà preso negli altri casi. Il tempo di “addestramento” di questo schema è superiore (deve “imparare” lo schema di ripetizione sia della storia locale che dei predittori, in totale 4 + 4 * 2 = 12 bit di informazione invece che 2), ma la capacità predittiva è migliore. In questo caso, il predittore ha una precisione del 100%, dove gli schemi precedenti si fermavano al 50% e al 75% rispettivamente.
Da notare che questo è vero solo se la lunghezza del ciclo è inferiore o uguale ai bit di storia accumulati nella BHT, altrimenti il predittore non ha abbastanza informazione per capire dove si trova all’interno del ciclo e sbaglierà di nuovo l’ultima iterazione del ciclo.
Aliasing
Fino a questo momento ho lasciato intendere che ogni branch ha il proprio predittore nel buffer, ma non è necessario che sia così; anzi, ci sono motivi per preferire il contrario. Consideriamo questo predittore… “particolare”:
La predizione viene fatta da un generatore casuale, senza alcuna correlazione col salto da eseguire. Naturalmente, il processore eseguirà comunque il programma correttamente! perchè i salti vengono comunque eseguiti e validati. Altrettanto ovviamente, le prestazioni di questo processore saranno penose.
Ma il punto è che, dato che il predittore può sbagliare, possiamo prenderci certe libertà architetturali. Ad esempio, il buffer potrebbe non avere tag: tutti i branch il cui indirizzo mappa sulla stessa entry nel buffer usano la stessa FSM, interferendo tra loro. Questo è chiamato aliasing; l’unica cosa che ci interessa è che l’aliasing sia abbastanza basso da avere un impatto trascurabile sulle prestazioni.
Eliminare le tag (e anche, ad esempio, i controlli ECC che invece troviamo nelle cache per evitare la possibile corruzione dei dati) permette di costruire buffer più piccoli e veloci, con effetti benefici sulle prestazioni.
Conclusione
In questo articolo ho illustrato alcune tecniche base usate per predire dinamicamente la direzione dei branch. Nel prossimo articolo descriverò alcune tecniche più sofisticate che permettono di ottenere precisioni ancora maggiori.