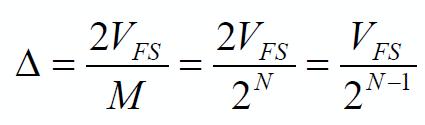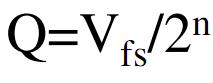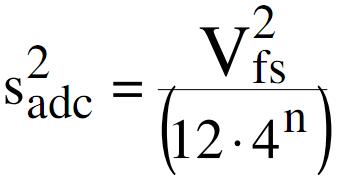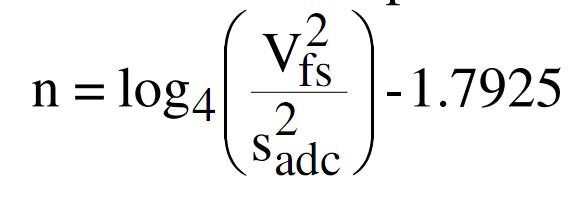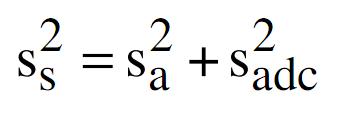
Nella scorsa puntata avevamo fatto la conoscenza con il processo di digitalizzazione di un segnale analogico ed avevamo fatto cenno agli errori che tale processo introduce. Oggi intendo approfondire questo aspetto, introducendo una differenziazione tra quantizzazione ideale e quantizzazione reale. Vale la pena di ricordare che un quantizzatore fornisce, in uscita, un valore numerico proporzionale ad una grandezza in ingresso che può essere, ad esempio, una tensione, oppure un valore di carica accumulato. La grandezza in ingrsso di un ADC è di tipo analogico e a scuola ci hanno insegnato che una grandezza analogica presenta un insieme continuo di valori. Entrare nel merito e menzionare quelle teorie che ipotizzano che lo spazio ed il tempo siano delle grandezze percepite come un continuum ma, nella realtà, discrete, non è lo scopo di questa trattazione; quindi mi limiterò a rifarmi alla definizione classica di grandezze continue e discrete senza timore di perdere di generalità o di rigore.
Terminata questa digressione, torniamo al processod i digitalizzazione di una grandezza continua. Quello che si deve fare è trasformare una curva in un aserie di valori numerici. Per farlo, si procede prima con l’individuazione di campioni significativi di quella curva che permettano di ricostruirne tutte le caratteristiche e le peculiarità, possibilmente senza perdere informazioni (ma abbiamo visto che questo non sempre è possibile). Questo primo passo è detto campionamento; il secondo step è quello di assegnare a ciascuno di questi campioni un valore numerico. Per farlo si definisocno una serie di intervalli, ognuno dei quali corrispondente ad uno dei campioni individuati e, ad ogni intervallo, si assegna un valore numerico. Appare evidente, a questo punto, che le quantità di intervalli (e quindi di campioni) e quello di valori numerici corrispondenti devono per lo meno, concidere, se non si vuole avere la certezza di perdere informazioni nell’eseguire la quantizzazione. A causa degli errori che introduconmo, le operazioni di campionamento e quantizzazione sono molto delicate e rappresentano il cuore dell’elaborazione numerica dei segnali.
Durante la quantizzazione, il primo errore che viene in mente è quello definito errore di quantizzazione, dovuto al tentativo di rappresentare una grandezza analogica con un numero finito di valori. Questo errore, chen è quello tipico di un quantizzatore ideale, è tanto maggiore quanto minore è il numero di bit utilizzato.
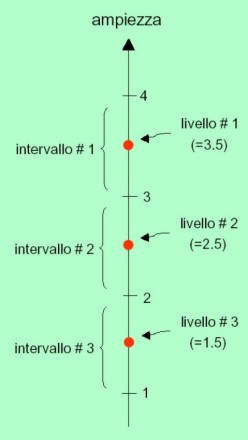
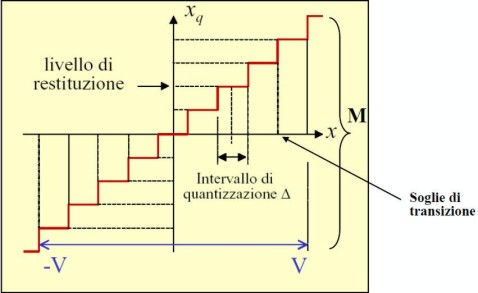
Ipotizzando una quantizzazione uniforme (ma le stesse considerazioni valgono anche per quelle non uniformi)
ponendo il valore di soglia al centro di ciscun livello
(nella seconda immagine si hanno solo 4 livelli, ovvero 2 bit ma non cambia nulla ai fini di ciò che si vuole dimostrare), si ha che, definendo con DELTA l’ampiezza di ciascun livello, con V(fs) la tensione massima di fondo scala, con N il numero di livelli, si ha che
ossia che la risoluzione, a parità di V(fs), aumenta all’aumnetare di N. La conclusione è ovvia, in quanto all’aumentare del numero di bit aumenta la quantoità di bit e, quindi, di informazione che siamo in grado di ricavare e di trasferire. In altre parole, si può dire che all’aumentare dell’informazione a disposizione, diminuisce lo scostamento dal segnale analogico originario a quello digitale sua rappresentazione, ovvero diminuisce l’errore di quantizzazione. Insomma, è come dire che un bel tramonto lo possiamo rappresentare meglio usando 8, 12, 14 o 16 bit per colore, piuttosto che 1 solo bit. La conseguenza logica potrebbe sembrare che è sufficiente aumentare il numero di bit per canale per avere una più fedele rappresentazione della realtà con il minor margine d’errore possibile. Quello ch sembra il classico uovo di Colombo (rigorosamente maiuscolo), presenta qualche inconveniente: innanzitutto più bit significanon anche più spazio occupato in memoria, più dati da trasferire (e quindi necessità di canali più veloci), più dati da elaborare (necessità di processori più veloci), ecc. Ma non è finita: il quantizzatore con cui abbiamo a che fare non è di tipo ideale e introduce altre componenti d’errore oltre quello di quantizzazione appena visto.
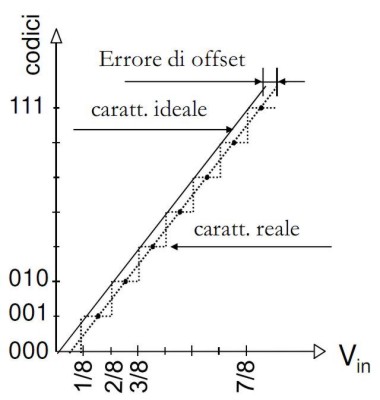
Il primo di questi errori è detto ERRORE DI OFFSET eprovoca una traslazione della caratteristica di conversione parallelamente a sé stessa, verso destra o verso sinistra,come mostrato in figura
Tutti i codici emessi sono modificati della stessa quantità; si tratta di un errore recuperabile mediante opportuna calibrazione che riporti i valori a coincidere o, quanto meno, a spostarsi il meno possibile dalla loro posizione ideale.
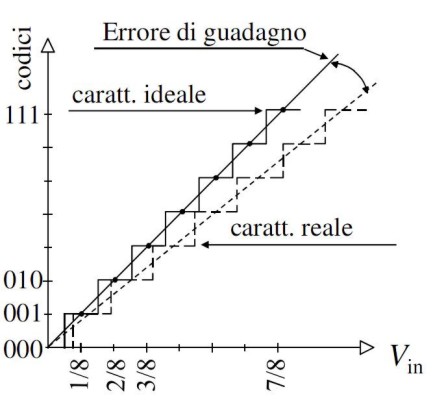
Il secondo errore tra quelli di tipo STATICO è l’ERRORE DI GUADAGNO che provoca una rotazione della caratteristica, in verso orario o antiorario, rispetto all’origine degli assi.
Tutti i codici emessi sono moltiplicati per la stessa quantità. Anche in questo caso si tratta di un errore recuperabile tramite opportuna compensazione.
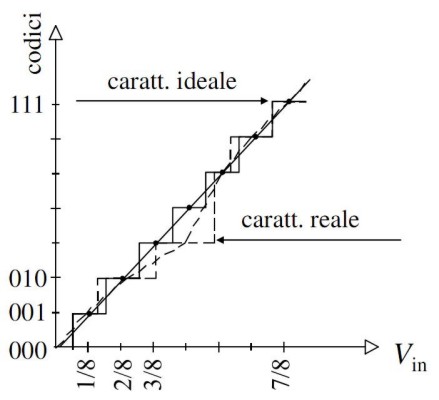
Il terzo tipo di erroe statico è il cosiddetto ERRORE DI NON LINEARITA’ DIFFERENZIALE che rappresenta l’errore, su ogni singola banda di quantizzazione, tra l’ampiezza di banda effettiva e quella ideale
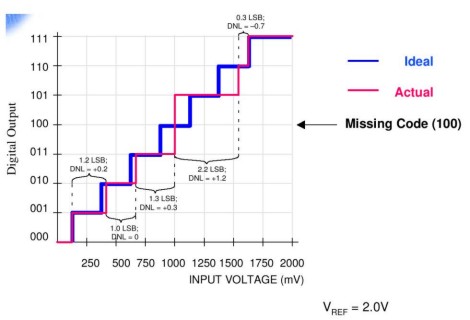
In tal caso, la caratteristica ha un andamento non lineare e può essere non monotona. Gli indici che definiscono la non linearità di un ADC sono 2 e si indicano con DNL (non linearità differenziale, appena visto) e INL (non linearità integrale). Un elevato valore di non linearità differenziale, tale da superare, per una determinata banda, l’ampiezza dell’intervallo dedicato ad un codice, può portare alla perdita di quel codice e, quindi, di parte dell’informazione, inducendo l’errore di OMISSIONE DI CODICE
Se la non linearità differenziale, per una determinata banda, è indice dello scostamento tra valore reale e valore ideale per quell’intervallo e può essere differente per ciscun livello di quantizzazione, la NON LINEARITA’ INTEGRALE è la somma di tutti questi scostamenti sull’intero campo di misura del’ADC.
Gli indici INL e DNL forniscono utili informazioni sul comportamento del quantizzatore:
- un elevato valore di INL indica che gli errori di non linearità differenziale tendono a deformare la caratteristica tutti o quasi nella stessa direzione
- un elevato valore di DNL ed un basso valore di INL, invece, sono indice del fatto che gli errori di non linearità sono elavati nei singoli intervalli della caratteristica, ma hanno segno opposto e tendono a compensarsi una volta sommati.
Anche gli errori dovuti alla non linearità possono, in qualche misura, essere trattati. Per ridurne gli effetti, si pensò di introdurre un rumore bianco da sommare al segnale. Nel 1960, Widrow scoprì che questo metodo era più efficace se il rumore bianco ed il segnale erano scorrelati. In un secondo tempo, furono individuate anche le caratteristiche che questo rumore doveva avere, a seconda del tipo di caratteristica del quantizzatore; questa tecnica è detta DITHERING. In particolare, ad esempio, per ADC con caratteristica di trasferimento simile all’ideale, è indicato un dither di tipo rumore bianco, mentre, per ACD con valori di DNL piuttosto significativi, è preferibile un segnale di dither a banda stretta, centrato sulla frequenza di Nyquist.
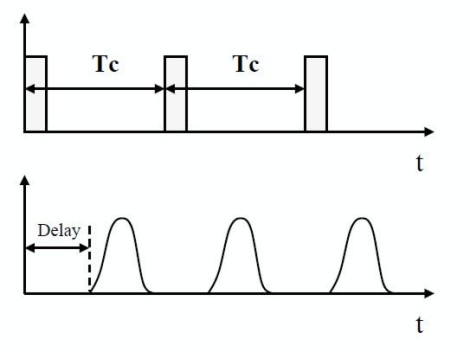
Non vi ammorbo oltre con considerazioni sul dithering e relative equazioni e passo a citare l’ultima tipologia di rumori introdotti dal processo di quantizzazione, quelli detti di TIPO DINAMICO e dovuti al fatto che i campioni non sono prelevati negli istanti prefissati a causa di:
- non idealità di ogni singolo impulso
- ritardo del treno di impulsi
Termino l’articolo di questa settimana citando un paio di parametri caratteristici di un convertitore A/D: il primo è il rapporto segnale/rumore o SNR; in un quantizzatore ideale, il SNR migliora all’aumentare del numero N di bit utilizzati. L’altro parametro, probabilmente meno noto, è il NUMERO EFFETTIVO DI BIT o ENOB (effective number of bits). Questo parametro ingloba anche le altre componenti di rumore e non solo l’errore di quantizzazione.
Ma vediamo come si comporta un quantizzatore reale all’aumentare del numero di bit utilizzati. Detta Q l’ampiezza del singolo intervallo, V(fs) la tensione di fondo scala e S(adc) la varianza del rumore di un quantizzatore ideale in cui compare il solo rumore di quantizzazione, si ha che
dove n è il numero di bit del convertitore; ricavando n, si ottiene
Se, però, non siamo nel caso ideale e, oltre al rumore di quantizzazione sono presenti tutti i tipi di rumore caratteristici di un quantizzaore reale e, in più, tutti i tipi di rumore visti nelle precedenti puntate generati a monte del cpnvertitore A/D, la varianza del rumore diventa
dove S(a) è il termine che tiene conto della non idealità dell’intero sistema. Come detto, all’aumentare di n, diminuisce S(adc) ma non S(a). Avere uan differente varianza comporta anche avere un diverso valore di n, ossia un numero effettivo di bit che può differire da quello ideale in misura tanto più grande quanto maggiore sarà la componente di “rumore non ideale”.
Ora, se quest’ultimo è trascurabile rispetto alla varianza ideale, ossia se si è riusciti a contenere al meglio il rumore, allora il numero bit effettivo e quello ideale coincideranno (o, comunque, le loro differenze saranno impercettibili); in caso contrario, il numero di bit effettivi potrà, all’aumentare del rumore totale, essere di molto inferiore al valore ideale.
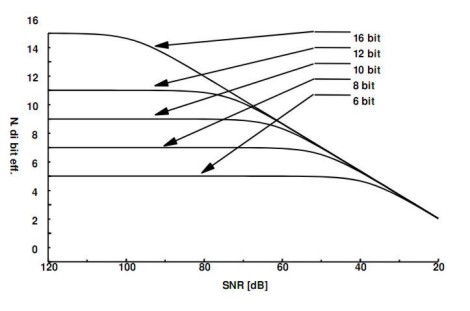
Molte delle tipologie di rumore passate in rassegna, rendono il sistema più vulnerabile al diminuire delle dimensioni del singolo intervallo di campionamento perchè rendono più facile un errorre di soglia o di omissione di codice. Quindi, all’aumentare del numero di bit bisognerà prestare la massima attenzione a queste componenti di rumore non ideale che possono rendere inutile lo sforzo fatto per conseguire una maggior precisione nelle operazioni di conversione. Per finire, andiamo proprio a gettare uno sguardo sulla tabella che fornisce l’andamento qualitativo e quantitativo del numero di bit effettivi al variare del SNR
Come si può vedere, all’aumentare del rumore (e quindi al peggiorare del SNR) il vantaggio di avere, ad esempio, 16 bit anzichè 14 o 12, si riduce velocemente e la riduzione è tanto più rapida quanto più è elevato il numero di bit. Questo comporta che è inutile avere convertitori con elevata risoluzione nominale, in presenza di un’elevata cifra di rumore generata internamente o esternamente al dispositivo di campionmento e quantizzazione e che, all’aumentare del numero di bit, ovvero della risoluzione nominale, per poter avere reali benefici è necessario implementare circuiti e relati algoritmi di filtraggio del rumore sempre più sofisticati e costosi.
Alla luce di quanto visto, appare chiaro il fatto che una full frame o, meglio ancora, una medio formato, a parità di algoritmi di NR, si avvantaggeranno, dell’uso di 14 o 16 bit, più di quanto non possa fare una apc-c, per non parlare di compatte e bridge superzoom.
Abbiamo, dunque, visto, come un sensore di dimensioni maggiori, fornisca indubbi vantaggi a livello di gestione del rumore, di contenimento degli effetti della diffrazione e di gamma dinamica. Nel prossimo capitolo vedremo gli effetti del rumore al variare della frequenza